Cho hai số tự nhiên a và b tùy ý có số dư trong phép chia cho 9 số deo thứ tự là r1, r2 và ab có cùng số dư trong phép chia cho 9.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a chia 9 dư r1 => a = 9p + r1 ( p là thương trong phép chia a cho 9 )
b chia 9 dư r2 => b = 9q + r2 ( q là thương trong phép chia b cho 9 )
Khi đó : ab = ( 9p + r1 )( 9q + r2 )
= 81pq + 9pr2 + 9qr1 + r1r2
gồi đến đây không biết trình bày sao :v nhờ các idol làm tiếp dùm em :))

\(a,b\)khi chia cho \(9\)được dư là \(r_1,r_2\)nên
\(a=9k+r_1,b=9l+r_2\).
\(ab=\left(9k+r_1\right)\left(9l+r_2\right)=81kl+9kr_2+9lr_1+r_1r_2\)
Có \(81kl,9kr_2,9lr_1\)đều chia hết cho \(9\)nên dư của phép chia \(ab\)cho \(9\)cũng là dư của \(r_1r_2\)khi chia cho \(9\).
Ta có đpcm.

Số dư trong phép chia là số dư lớn nhất nên kém số chia 1 đơn vị.
Ta có sơ đồ sau:
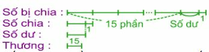
Theo sơ đồ, nếu gọi số chia là 1 phần, thêm 1 đơn vị vào số dư và số bị chia thì tổng số phần của số chia, số bị chia và số dư (mới) gồm : 15 + 1 + 1 + 1 = 18 (phần) như vậy. Khi đó tổng của số chia, số bị chia và số dư (mới) là : 769 - 15 + 1 + 1 = 756.
Số chia là : 756 : 18 = 42
Số dư là : 42 - 1 = 41
Số bị chia là : 42 x 15 + 41 = 671