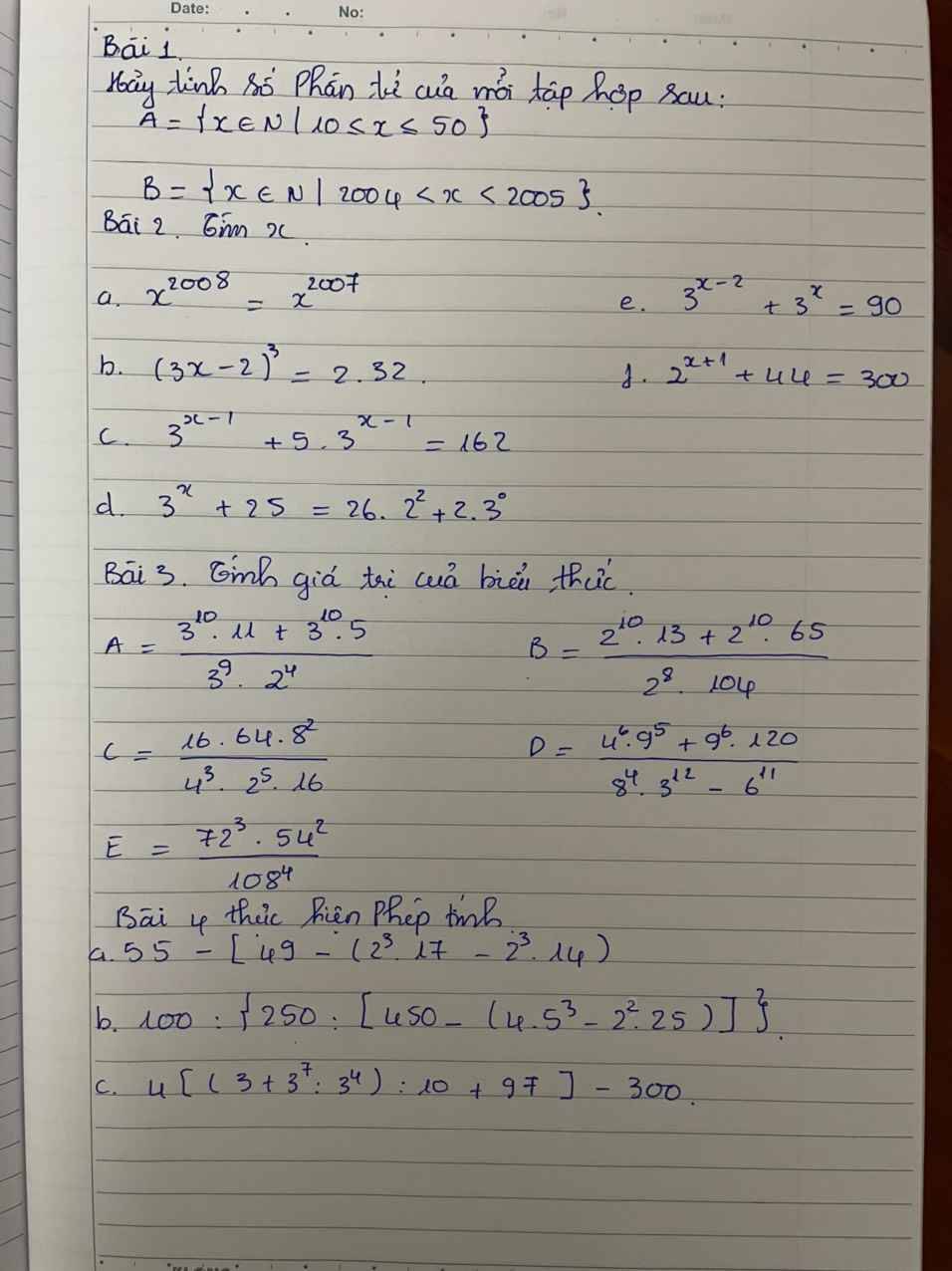
Câu c bài 2. Mình đang cần gấp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NC
0
A
2
3 tháng 9 2021
a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
câu c với , mình đang cần gấp
em mới lớp 5 sai thì bỏ qua nhé!30 tháng 10 2021
Bài kiểm tra tôt snhaats dựa vào câu trl khác đi, lớp 5 ko rõ bằng lớp 7 đâu!
QN
3
5 tháng 9 2021
\(a,A=x^2-6x-2=\left(x-3\right)^2-11\ge-11\)
Dấu \("="\Leftrightarrow x=3\)
\(b,B=6x-9x^2+2=-\left(3x-1\right)^2+3\le3\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{3}\)
TL
0
BH
7
26 tháng 2 2022
Simple answer, but not true
I disguise Santa Claus/ Father Christmas.
NP
0
DN
3
19 tháng 9 2020
Ngoài ba dạng thông tin cơ bản nêu trong bài học, còn có những dạng thông tin khác như:
- Thông tin truyền miệng
- Thông tin thẩm mỹ
- Thông tin khoa học
- Thông tin dấu tích
- Thông tin hành động
