cho a,b,c là 3 số thực thỏa mãn: a+b+c=a3+b3+c3=0
tính giá trị biểu thức: P= a2021+b2021+c2021
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 2 2022
Do \(0\le a,b,c\le1\)
nên\(\left\{{}\begin{matrix}\left(a^2-1\right)\left(b-1\right)\ge0\\\left(b^2-1\right)\left(c-1\right)\ge0\\\left(c^2-1\right)\left(a-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b-b-a^2+1\ge0\\b^2c-c-b^2+1\ge0\\c^2a-a-c^2+1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b\ge a^2+b-1\\b^2c\ge b^2+c-1\\c^2a\ge c^2+a-1\end{matrix}\right.\)
Ta cũng có:
\(2\left(a^3+b^3+c^3\right)\le a^2+b+b^2+c+c^2+a\)
Do đó \(T=2\left(a^3+b^3+c^3\right)-\left(a^2b+b^2c+c^2a\right)\)
\(\le a^2+b+b^2+c+c^2+a\)\(-\left(a^2+b-1+b^2+c-1+c^2+a-1\right)\)
\(=3\)
Vậy GTLN của T=3, đạt được chẳng hạn khi \(a=1;b=0;c=1\)
CM
11 tháng 1 2018
Đáp án C
Nhận xét, với x ∈ [1;2] thì f(x) = x - log2x ≤ 0. Thật vậy, xét f ' ( x ) = x ln 2 - 1 x ln 2
Từ đây suy ra
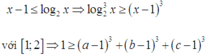
Mặt khác cũng có
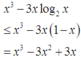
với [1;2]
CM
8 tháng 2 2019
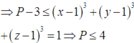
Đáp án C
Nhận xét, với x ∈ 1 ; 2 thì f x = x − log 2 x ≤ 0 . Thật vậy, xét f ' x = x ln 2 − 1 x ln 2
→ f ' x = 0 ⇔ x = 1 ln 2 ⇒ max 1 ; 2 f x = max f 1 , f 1 ln 2 , f 2 = 0
Từ đây suy ra x − 1 ≤ log 2 x ⇒ log 2 3 x ≥ x − 1 3 với 1 ; 2 ⇒ 1 ≥ a − 1 3 + b − 1 3 + c − 1 3
Mặt khác cũng có x 3 − 3 x log 2 x ≤ x 3 − 3 x 1 − x = x 3 − 3 x 2 + 3 x với 1 ; 2
⇒ P − 3 ≤ x − 1 3 + y − 1 3 + z − 1 3 = 1 ⇒ P ≤ 4
AH
Akai Haruma
Giáo viên
12 tháng 2 2022
Lời giải:
Tìm min:
Áp dụng BĐT AM-GM:
$a^3+a^3+1\geq 3a^2$
$b^3+b^3+1\geq 3b^2$
$c^3+c^3+1\geq 3c^2$
$\Rightarrow 2(a^3+b^3+c^3)+3\geq 3(a^2+b^2+c^2)$
$\Leftrightarrow 2P+3\geq 9$
$\Leftrightarrow P\geq 3$
Vậy $P_{\min}=3$ khi $(a,b,c)=(1,1,1)$
----------------
Tìm max:
$a^2+b^2+c^2=3\Rightarrow a^2,b^2,c^2\leq 3$
$\Rightarrow a,b,c\leq \sqrt{3}$
Do đó: $a^3-\sqrt{3}a^2=a^2(a-\sqrt{3})\leq 0$
$\Rightarrow a^3\leq \sqrt{3}a^2$
Tương tự với $b,c$ và cộng theo vế:
$P\leq \sqrt{3}(a^2+b^2+c^2)=3\sqrt{3}$
Vậy $P_{\max}=3\sqrt{3}$ khi $(a,b,c)=(\sqrt{3},0,0)$ và hoán vị.
CM
31 tháng 5 2019
Đáp án C.
Đặt log 2 a = x log 2 b = y log 2 c = z ⇒ a = 2 x b = 2 y c = 2 z ⇒ P = 2 x 3 + 2 y 3 + 2 z 3 − 3 x .2 x + y .2 y + z .2 z ,
trong đó x 3 + y 3 + z 3 ≤ 1 và x , y , z ∈ 0 ; 1 .
Dễ chứng minh được 2 x ≤ x + 1 , ∀ x ∈ 0 ; 1 . Dấu “=” xảy ra ⇔ x = 0 ∨ x = 1 .
Suy ra
2 x − x 3 ≤ 1 ⇔ 2 x 3 ≤ 3. 2 x 2 . x − 3.2 x . x 2 + x 3 + 1 ⇒ 2 x 3 − 3 x .2 x ≤ 3 x .2 x 2 x − x − 1 + x 3 + 1 ≤ x 3 + 1 Từ đó suy ra P ≤ x 3 + 1 + y 3 + 1 + z 3 + 1 ≤ 4 .
Dấu bằng xảy ra khi trong ba số x , y , z có 1 số bằng 1 và hai số còn lại bằng 0. Do đó chọn C.
\(a+b+c=0\)
\(\Rightarrow\left(a+b+c\right)^3=0\)
\(\Rightarrow\left(a+b\right)^3+3\left(a+b\right)c\left(a+b+c\right)+c^3=0\)
\(\Rightarrow a^3+b^3+c^3+3\left(a+b\right)\left(ac+bc+c^2\right)+3ab\left(a+b\right)=0\)
\(\Rightarrow3\left(a+b\right)\left(ac+bc+c^2+ab\right)=0\)
\(\Rightarrow3\left(a+b\right)\left[c\left(b+c\right)+a\left(b+c\right)\right]=0\)
\(\Rightarrow3\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=-b\\b=-c\\c=-a\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}c=0\\a=0\\b=0\end{matrix}\right.\)
*\(a=-b;c=0\Rightarrow P=a^{2021}-a^{2021}+0^{2021}=0\)
*\(b=-c;a=0\Rightarrow P=0^{2021}+b^{2021}-b^{2021}=0\)
*\(c=-a;b=0\Rightarrow P=a^{2021}+0^{2021}-a^{2021}=0\)
Vậy \(P=0\)