Câu 6 làm sao vậy ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`2/(x+1)+x/(3x+3)=1`
`ĐK:x ne -1`
`pt<=>6/(3x+3)+x/(3x+3)=1`
`<=>(x+6)/(3x+3)=1`
`<=>x+6=3x+3`
`<=>2x=2`
`<=>x=1(TM)`
Vậy pt có 1 nghiệm

vì sao nó lên câu trả lời để mình hỏi mà sao nó cứ lên mua tài khoản vid

Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.

bn bam vao cau hoi toi quan tam va tim cau bn muon xoa roi bam chinh sua het la xong
Thiện tai,thiện tai...
Những lỗi lầm của thí chủ không dễ dàng xóa đi dc đâu.
Nam mô...


Giải:
a) Vì Om là tia p/g của xÔy
⇒xÔm=mÔy=xÔy/2=40o/2=20o
Vì On là tia p/g của xÔz
⇒xÔn=nÔz=xÔz/2=120o/2=60o
⇒xÔy+yÔn=xÔn
40o +yÔn=60o
yÔn=60o-40o
yÔn=20o
⇒mÔy+yÔn=mÔn
20o +20o =mÔn
⇒mÔn=40o
b) Vì +) mÔy+yÔn=mÔn
+) mÔy=yÔn=20o
⇒Oy là tia p/g của mÔn
c) Vì tia Ot là tia đối của tia Oy
⇒yÔt=180o
Vì +) Oy;Oz cùng ∈ 1 nửa mặt phẳng có bờ chứa tia Ox
+) xÔy<xÔz (40o<120o)
⇒Oy nằm giữa Ox và Oz
⇒xÔy+yÔz=xÔz
40o+yÔz=120o
yÔz=120o-40o
yÔz=80o
⇒yÔz+zÔt=180o (2 góc kề bù)
80o+zÔt=180o
zÔt=180o-80o
zÔt=100o
Chúc bạn học tốt!


`a)`
Cho `x^2-4=0`
`=>x^2=4`
`=>x^2=2^2` hoặc `x^2=(-2)^2`
`=>x=2` hoặc `x=-2`
Vậy nghiệm của đa thức là `x=2` hoặc `x=-2`
______________________________________
`b)` Cho `2x^2-x=0`
`=>x(2x-1)=0`
`@TH1:x=0`
`@TH2:2x-1=0=>2x=1=>x=1/2`
Vậy nghiệm của đa thức là `x=0` hoặc `x=1/2`


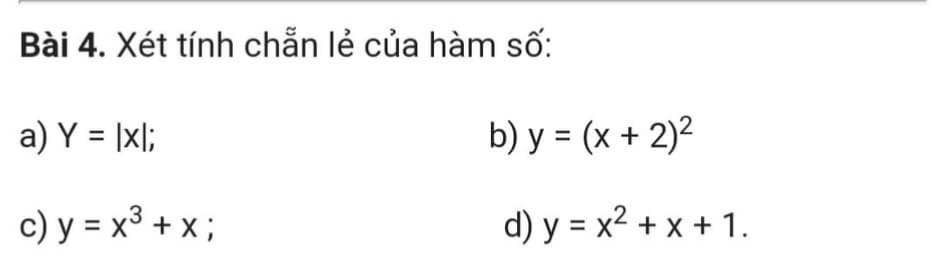



\(\overrightarrow{MN}=\left(2;2\right)\Rightarrow MN=\sqrt{2^2+2^2}=2\sqrt{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\sqrt{2}\)
Gọi I là tâm đường tròn đường kính MN \(\Rightarrow\) I là trung điểm MN
\(\Rightarrow I\left(0;2\right)\)
Phương trình (C): \(x^2+\left(y-2\right)^2=2\)
b.
Tiếp tuyến d' song song d nên nhận \(\left(3;-5\right)\) là 1 vtpt
Phương trình d' có dạng: \(3x-5y+c=0\)
d' là tiếp tuyến của (C) nên: \(d\left(I;d'\right)=R\)
\(\Leftrightarrow\dfrac{\left|3.0-5.2+c\right|}{\sqrt{3^2+\left(-5\right)^2}}=\sqrt{2}\Leftrightarrow\left|c-10\right|=2\sqrt{17}\)
\(\Rightarrow\left[{}\begin{matrix}c=10+2\sqrt{17}\\c=10-2\sqrt{17}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}3x-5y+10+2\sqrt{17}=0\\3x-5y+10-2\sqrt{17}=0\end{matrix}\right.\)