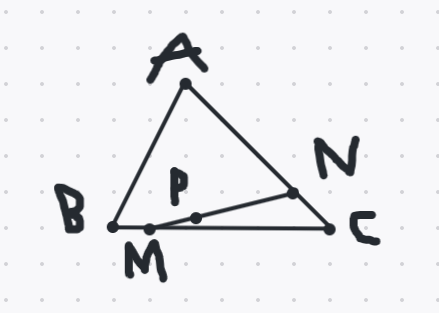
Cho ΔABC, điểm M nằm trên cạnh BC sao cho BC gấp 5 lần BM;
Điểm N trên cạnh AC sao cho AN = 3/4 AC.
a) Tính diện tích ΔMNC, biết diện tích ΔABC bằng 35 cm2.
b) Lấy điểm P trên đoạn MN sao cho NP = 2/3 NM. So sánh diện tích ΔAMP và ΔABM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Ta có
\(BC=5xBM\Rightarrow BM=\dfrac{1}{5}xBC\Rightarrow CM=BC-BM=BC-\dfrac{1}{5}xBC=\dfrac{4}{5}xBC\)
\(AN=\dfrac{3}{4}xAC\Rightarrow CN=AC-AN=AC-\dfrac{3}{4}xAC=\dfrac{1}{4}xAC\)
Hai tg AMC và tg ABC có chungg đường cao từ A->BC nên
\(\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{CM}{BC}=\dfrac{4}{5}\Rightarrow S_{AMC}=\dfrac{4}{5}xS_{ABC}\)
Hai tg ACM và tg MNC có chung đường cao từ M->AC nên
\(\dfrac{S_{MNC}}{S_{AMC}}=\dfrac{CN}{AC}=\dfrac{1}{4}\Rightarrow S_{MNC}=\dfrac{1}{4}xS_{AMC}=\dfrac{1}{4}x\dfrac{4}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}=\dfrac{1}{5}x35=7cm^2\)
b/
\(S_{AMN}=S_{AMC}-S_{MNC}=\dfrac{4}{5}xS_{ABC}-\dfrac{1}{5}xS_{ABC}=\dfrac{3}{5}xS_{ABC}\)
Ta có
\(NP=\dfrac{2}{3}xNM\Rightarrow MP=NM-NP=NM-\dfrac{2}{3}xNM=\dfrac{1}{3}xNM\)
Hai tg AMP và tg AMN có chung đường cao từ A->NM nên
\(\dfrac{S_{AMP}}{S_{AMN}}=\dfrac{MP}{NM}=\dfrac{1}{3}\Rightarrow S_{AMP}=\dfrac{1}{3}xS_{AMN}=\dfrac{1}{3}x\dfrac{3}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}\)
Ta có
\(S_{ABM}=S_{ABC}-S_{ACM}=S_{ABC}-\dfrac{4}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}\)
\(\Rightarrow S_{AMP}=S_{ABM}\)

tham khảo
Ta có : BM/BC=1/5 => dtAMB=1/5dtABC (1)
Ta lại có : NP=/MN=2/3 =>MP/MN=1/3 => dtAMP=1/3dtAMN (2)
Ta có -AN/AC=3/4 =>dtAMN=3/4dtAMC
-MC/BC=4/5 =>dtAMC=4/5dtABC
=>dtAMN=3/5dtABC (3)
Từ (2) và (3) => dtAMP=1/5 dtABC (4)
Từ (1) và (4) =>dtAMB=dtAMP

Ta có : BM/BC=1/5 => dtAMB=1/5dtABC (1)
Ta lại có : NP=/MN=2/3 =>MP/MN=1/3 => dtAMP=1/3dtAMN (2)
Ta có -AN/AC=3/4 =>dtAMN=3/4dtAMC
-MC/BC=4/5 =>dtAMC=4/5dtABC
=>dtAMN=3/5dtABC (3)
Từ (2) và (3) => dtAMP=1/5 dtABC (4)
Từ (1) và (4) =>dtAMB=dtAMP
a: S ABM=1/5*35=7cm2
S AMC=28cm2
=>S AMN=21cm2
=>S MNC=7cm2
b:S AMP=21*1/3=7cm2
S ABM=7cm2
=>S AMP=S ABM