cho 3 số 9x,4y,\(3\sqrt{x}+2\sqrt{y}\) là các số hữu tỉ. Chứng minh rằng \(\sqrt{x},\sqrt{y}\)là các số hữu tỉ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 8 2020
Với x = y \(\ge\)0=> \(\sqrt{x}=\sqrt{y}\) là số hữu tỉ
Với \(x\ne y>0\)
Đặt \(\sqrt{x}+\sqrt{y}=t\) là số hữu tỉ
=> \(\frac{x-y}{\sqrt{x}-\sqrt{y}}=t\Rightarrow\sqrt{x}-\sqrt{y}=\frac{x-y}{t}\) là số hữu tỉ
=> \(\sqrt{x};\sqrt{y}\) là số hữu tỉ
20 tháng 5 2017
Điều kiện \(\hept{\begin{cases}x\ge0\\y\ge0\end{cases}}\)
\(1+\sqrt{x+y+3}=\sqrt{x}+\sqrt{y}\)
\(\Leftrightarrow\sqrt{x+y+3}=\sqrt{x}+\sqrt{y}-1\) (\(\sqrt{x}+\sqrt{y}-1>0\))
\(\Leftrightarrow\sqrt{x}+\sqrt{y}-\sqrt{xy}+1=0\)
\(\Leftrightarrow\sqrt{x}+\sqrt{y}=\sqrt{xy}-1\) (\(\sqrt{xy}-1>0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2=\left(\sqrt{xy}-1\right)^2\)
\(\Leftrightarrow4\sqrt{xy}=x+y-xy-1\)
Vì x, y nguyên nên \(\sqrt{xy}\) cũng phải nguyên
\(\Rightarrow\sqrt{x}+\sqrt{y}=\sqrt{xy}-1\) nguyên (1)
Ta lại có:
\(x-y=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)\)
\(\Rightarrow\sqrt{x}-\sqrt{y}\) nguyên (2)
Lấy (1) + (2) và (1) - (2) ta có:
\(\hept{\begin{cases}\sqrt{x}+\sqrt{y}+\sqrt{x}-\sqrt{y}=2\sqrt{x}\\\sqrt{x}+\sqrt{y}-\sqrt{x}+\sqrt{y}=2\sqrt{y}\end{cases}}\)
\(\Rightarrow\sqrt{x},\sqrt{y}\) là số nguyên
Vậy x, y là bình phương đúng của 1 số nguyên.
AH
Akai Haruma
Giáo viên
17 tháng 7 2018
Lời giải:
Đặt \(\sqrt{x}+\sqrt{y}=a\in\mathbb{Q}\)
\(\Rightarrow \sqrt{x}=a-\sqrt{y}\)
Bình phương 2 vế:
\(x=a^2+y-2a\sqrt{y}\)
\(\Rightarrow 2a\sqrt{y}=a^2+y-x\in\mathbb{Q}\) do \(a,x,y\in\mathbb{Q}\)
Ta thấy \(\left\{\begin{matrix} 2a\sqrt{y}\in\mathbb{Q}\\ 2a\in\mathbb{Q}\end{matrix}\right.\Rightarrow \sqrt{y}\in\mathbb{Q}\)
\(\left\{\begin{matrix} \sqrt{x}+\sqrt{y}\in\mathbb{Q}\\ \sqrt{y}\in\mathbb{Q}\end{matrix}\right.\Rightarrow \sqrt{x}\in\mathbb{Q}\)
Ta có đpcm.
20 tháng 11 2019
Đẳng thức đã cho tương đương với
\(x^2+2xy+y^2+\left(\frac{xy+1}{x+y}\right)^2=2+2xy.\)
\(\Leftrightarrow\left(x+y\right)^2+\left(\frac{xy+1}{x+y}\right)^2-2\left(xy+1\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2-2\left(x+y\right).\frac{xy+1}{x+y}+\left(\frac{xy+1}{x+y}\right)^2=0\)
\(\Leftrightarrow\left(x+y-\frac{xy+1}{x+y}\right)^2=0\)
\(\Leftrightarrow x+y-\frac{xy+1}{x+y}=0\)
\(\Leftrightarrow\left(x+y\right)^2=xy+1\)
\(\Leftrightarrow\sqrt{1+xy}=|x+y|\)
Vì x,y là số hữu tỉ nên Vế phải của đẳng thức là số hữu tỉ => Điều phải chứng minh
30 tháng 5 2021
\(ĐKXĐ:x\ge0;y\ge0\)
Ta có:\(pt\Rightarrow2\sqrt{3}-3=\sqrt{3}x+\sqrt{3}y-6xy\)
\(\Leftrightarrow\sqrt{3}\left(x+y-2\right)=3\left(2xy-1\right)\)
\(\Leftrightarrow x+y-2=\sqrt{3}\left(2xy-1\right)\)
Nếu \(2xy-1\ne0\),ta có:
\(\Rightarrow\sqrt{3}=\frac{x+y-2}{2xy-1}\inℚ\left(L\right)\)
Do đó:2xy-1=0,từ đó suy ra x+y-2=0,do đó ta có hệ phương trình:
\(\hept{\begin{cases}2xy-1=0\\x+y-2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}xy=\frac{1}{2}\\x+y=2\end{cases}\Leftrightarrow}\hept{\begin{cases}xy=\frac{1}{2}\\x=2-y\end{cases}\Leftrightarrow\left(2-y\right)y=\frac{1}{2}}\)
\(\Leftrightarrow y^2-2y+\frac{1}{2}=0\Leftrightarrow\left(y-1\right)^2=\frac{1}{2}\Rightarrow\orbr{\begin{cases}y-1=\frac{1}{\sqrt{2}}\\y-1=-\frac{1}{\sqrt{2}}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}y=1+\frac{1}{\sqrt{2}}\Rightarrow x=1-\frac{1}{\sqrt{2}}\\y=1-\frac{1}{\sqrt{2}}\Rightarrow x=1+\frac{1}{\sqrt{2}}\end{cases}}\left(TM\right)\)
Vậy tập nghiệm của pt là:\(\left(x,y\right)=\left\{\left(1-\frac{1}{\sqrt{2}};1+\frac{1}{\sqrt{2}}\right),\left(1+\frac{1}{\sqrt{2}};1-\frac{1}{\sqrt{2}}\right)\right\}\)
HM
28 tháng 9 2016
xét 1-1/xy:
=(xy-1)/xy
nhân 4x^3y^3 vào bt:
(4x^4y^4-4x^3y^3)/4x^4y^4
thay 4x^4y^4=(x^3+y^3)^2:
=[(x^3+y^3)^2-4x^3y^3]/(x^3+y^3)^2
=(x^6+y^6-2x^3y^3)/(x^3+y^3)^2
=(x^3-y^3)^2/(x^3+y^3)^2
=>căn(1-1/xy)=lx^3-y^3l / lx^3+y^3l là số hữu tỉ
BT
28 tháng 9 2016
Cô phải đọc rất kĩ mới hiểu bài của Minh. Lần sau em chú ý dùng công thức có trong phần \(f\left(x\right)\)để bài làm được trực quan hơn.
Cảm ơn em đã trình bày bài giải !
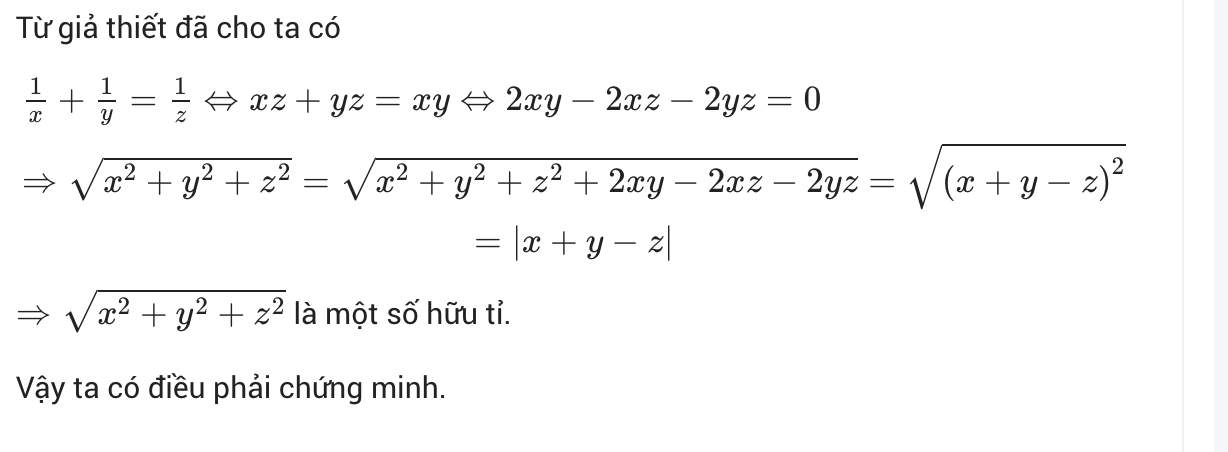
Ta có \(9x-4y=\left(3\sqrt{x}-2\sqrt{y}\right)\left(3\sqrt{x}+2\sqrt{y}\right)\)là số hữu tỷ
Vì \(\left(3\sqrt{x}-2\sqrt{y}\right)\)(1) là số hữu tỷ nên \(\left(3\sqrt{x}+2\sqrt{y}\right)\)(2) cũng là số hữu tỷ
Lấy (2) - (1) và (2) + (1) ta được
\(\hept{\begin{cases}4\sqrt{y}\\6\sqrt{x}\end{cases}}\)là 2 số hữu tỷ vậy \(\sqrt{x},\sqrt{y}\)là hai số hữu tỷ