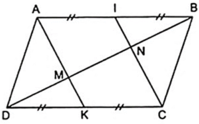
Cho hình bình hành ABCD gọi K và I lần lượt là trung điểm của AB và CD.
1. Chứng minh AI=CK
2. AI cắt BD tại M , CK cắt BD tại N .Chứng minh DM=1/3 BD
3. Chứng minh BD , AC và IK đồng quy tại một điểm
giúp mk với!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: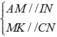
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
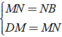 ⇒ DM = MN = NB
⇒ DM = MN = NB

a ) AK = 1/2 AB
CI = 1/2 CD
Mà AB //= CD nên AK //= CI suy ra
AKCI - hình bình hành
Nên AI // CK
b ) Xét t/g DNC có :
I là trung điểm CD mà IM // NC
=> IM là đường trung bình của t/g DNC
=> MD = MN ( 1 )
Xét t/g ABM có :
K là trung điểm AB mà KN // AM
=> KN là đường trung bình của t/g ABM ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra DM = MN = NB

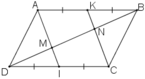
a) + K là trung điểm của AB ⇒ AK = AB/2.
+ I là trung điểm của CD ⇒ CI = CD/2.
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = CD/2 hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI//KC hay MI//NC.
ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)
+ AI // KC hay KN//AM
ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra:AN//CM

a: Xét tứ giác AECK có
AK//EC
AK=EC
Do đó: AECK là hình bình hành
1/ Ta có AB//=CD (t/c hình bình hành)
KA=KB; IC=ID (đề bài)
=> AK//=IC => AKCI là hình bình hành => AI//CK
2/ Từ AI//CK và KB=KA theo talet
\(\Rightarrow\frac{KB}{KA}=\frac{NB}{NM}=1\Rightarrow NB=NM\left(1\right)\)
Từ AI//CK và ID=IC theo talet
\(\Rightarrow\frac{ID}{IC}=\frac{MD}{NM}=1\Rightarrow MD=MN\left(2\right)\)
Mà BD = MD + NM + NB (3)
Từ (1) (2) và (3) => MD=NM=NB => \(DM=\frac{BD}{3}\)
3/ Gọi O là giao của AC và BD
Do ABCD là hình bình hành => BD cắt BC tại O là trung điểm của AC (t/c đường chéo hbh)
Do AKCI là hình bình hành => IK cắt BC tại trung điểm O của BC (t/c đường chéo hbh)
=> BD; AC; IK đồng qui tại O