Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

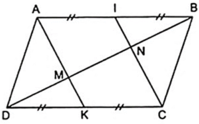
Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: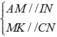
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
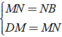 ⇒ DM = MN = NB
⇒ DM = MN = NB

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra:AN//CM

a ) AK = 1/2 AB
CI = 1/2 CD
Mà AB //= CD nên AK //= CI suy ra
AKCI - hình bình hành
Nên AI // CK
b ) Xét t/g DNC có :
I là trung điểm CD mà IM // NC
=> IM là đường trung bình của t/g DNC
=> MD = MN ( 1 )
Xét t/g ABM có :
K là trung điểm AB mà KN // AM
=> KN là đường trung bình của t/g ABM ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra DM = MN = NB

Xin phép ad cho em tách ạ,nguyên 1 câu khá là dài,hihi


1/ Ta có AB//=CD (t/c hình bình hành)
KA=KB; IC=ID (đề bài)
=> AK//=IC => AKCI là hình bình hành => AI//CK
2/ Từ AI//CK và KB=KA theo talet
\(\Rightarrow\frac{KB}{KA}=\frac{NB}{NM}=1\Rightarrow NB=NM\left(1\right)\)
Từ AI//CK và ID=IC theo talet
\(\Rightarrow\frac{ID}{IC}=\frac{MD}{NM}=1\Rightarrow MD=MN\left(2\right)\)
Mà BD = MD + NM + NB (3)
Từ (1) (2) và (3) => MD=NM=NB => \(DM=\frac{BD}{3}\)
3/ Gọi O là giao của AC và BD
Do ABCD là hình bình hành => BD cắt BC tại O là trung điểm của AC (t/c đường chéo hbh)
Do AKCI là hình bình hành => IK cắt BC tại trung điểm O của BC (t/c đường chéo hbh)
=> BD; AC; IK đồng qui tại O