Cho hình lập phương ABCD.A1B1C1D1 có cạnh bằng 5 cm ơ Gọi A và A1 lần lượt là giao điểm của các đường chéo AC với BD và và A1 C1 một với B1 D1 a)Tính diện tích toàn phần và thể tích của hình lập phương b) Tính thể tích của hình chóp O1 .ABCD( kết quả làm tròn đến chữ số thập phân thứ nhất)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

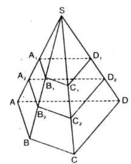
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
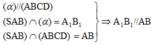
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
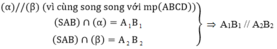
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D

Chọn C.
Diện tích toàn phần của hình lập phương là
![]()
Hình trụ có bán kính đáy là 20 cm và đường cao là 40 cm nên diện tích toàn phần của hình trụ là
![]()
![]()

Đáp án B
Bán kính đáy của hình trụ là R = 20 cm
Diện tích toàn phần của hình lập phương là S 1 = 6 . 40 2 = 9600 c m 2
Diện tích toàn phần của hình trụ là S 2 = 2 πRh + 2 πR 2 = 2 π 20 . 40 + 2 π 40 2 = 4800 cm 2
Vậy tổng S = S 1 + S 2 = 9600 + 4800 π = 2400 4 + 2 π cm 2

Đáp án C
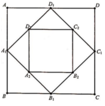
Diện tích hình vuông A B C D là S 1 = a 2 ; diện tích hình vuông A 1 B 1 C 1 D 1 là S 2 = a 2 2 2 = a 2 2
Diện tích hình vuông A 2 B 2 C 2 D 2 là a 2 2 = a 2 4 ; ...
Diện tích hình vuông A 99 B 99 C 99 D 99 là S 100 = a 2 2 99
Vậy S = a 2 1 2 0 + 1 2 1 + 1 2 2 + ... + 1 2 99 ⏟ T
với T là tổng của CSN có u 1 = 1 ; q = 1 2 và n = 100
Do đó, tổng:
S = a 2 . 1 − 1 2 100 1 − 1 2 = 2 a 2 1 − 1 2 100 = a 2 2 100 − 1 2 99

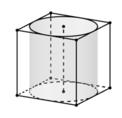
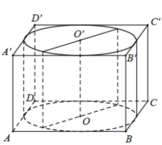




a) Diện tích xung quanh là: \(5^2.4=100\left(cm^2\right)\)
Diện tích toàn phần là: \(5^2.6=150\left(cm^2\right)\)
b) Thể tích khối chóp \(O_1.ABCD\) là: \(V=\dfrac{1}{3}.h.S_{ABCD}=\dfrac{1}{3}.5.5^2=\dfrac{125}{3}\left(cm^3\right)\)