Chứng minh phương trình 4x^2-4x+3=0 vô nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


anh ơi, vậy là sai đề hả anh, chứ đề kêu chứng minh phương trình vô nghiệm mà em thấy anh ghi x=2

\(\text{CM vô nghiệm}\)
\(\text{a) }\left(x-2\right)^3=\left(x-2\right).\left(x^2+2x+4\right)-6\left(x-1\right)^2\)
\(\Leftrightarrow x^3-6x^2+12x-8=x^3-8-6\left(x^2-2x+1\right)\)
\(\Leftrightarrow x^3-6x^2+12x-8=x^3-8-6x^2+12x-6\)
\(\Leftrightarrow x^3-6x^2+12x-x^3+6x-12x=-8+8-6\)
\(\Leftrightarrow0x=-6\text{ (vô lí)}\)
\(\text{Vậy }S=\varnothing\)
\(\text{b) }4x^2-12x+10=0\)
\(\Leftrightarrow\left(4x^2-12x+9\right)+1=0\)
\(\Leftrightarrow\left(2x-3\right)^2+1=0\)
\(\Leftrightarrow\left(2x-3\right)^2=-1\text{ (vô lí)}\)
\(\text{Vậy }S=\varnothing\)
\(\text{CM vô số nghiệm}\)
\(\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)^3-3x\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left[\left(x+1\right)^2-3x\right]\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(x^2+2x+1-3x\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(x^2-x+1\right)\text{ (luôn luôn đúng)}\)
\(\text{Vậy }S\inℝ\)

\(\left|x-2\right|+\left|x^2-4x+3\right|=0\)
\(\hept{\begin{cases}\left|x-2\right|\ge0\\\left|x^2-4x+3\right|\ge0\end{cases}\text{dấu }=\text{xảy ra khi }}\)
\(\hept{\begin{cases}\left|x-2\right|=0\\\left|x^2-4x+3\right|=0\end{cases}\Rightarrow\hept{\begin{cases}x-2=0\\x^2-4x+3=0\end{cases}}\Rightarrow\hept{\begin{cases}x=2\\\left(x-1\right).\left(x-3\right)=0\end{cases}\Rightarrow}\hept{\begin{cases}x=2\\x=1,x=3\end{cases}}}\)(vô lí)
Vậy phương trình vô nghiệm
p/s: mk ko bt cách trình bài => sai sót bỏ qua

1. x\(^4\)-x\(^3\)+2x\(^2\)-x+1=0
\(\Leftrightarrow\)(x^4-x^3+x^2) +(x^2-x+1)=0
\(\Leftrightarrow\)x^2(x^2-x+1) +(x^2-x+1)=0
\(\Leftrightarrow\)(x^2-x+1)(x^2+1)=0
\(\Leftrightarrow\)\([\)(x^2-x+1/4)+3/4\(]\)(x^2+1)=0
\(\Leftrightarrow\)\([\)(x-1/2)\(^2\)+3/4\(]\)(x^2+1)=0
VÌ (x-1/2)\(^2\)+3/4>0\(\forall\)x
x^2+1>0\(\forall\)x
\(\Rightarrow\)Phương trình đã cho vô nghiệm
1)x^4 - x^3 + 2x^2 - x + 1 = 0
(x^4 + 2x^2 +1) - (x^3+x)= 0
x^4 + 2x^2 + 1 = x^3 - x
(x^2 + 1)^2 = x(x^2 + 1)
(x^2+1)(x^2+1) = x(x^2 + 1)
(x^2+1)(x^2+1) = x(x^2 + 1)
x^2+1 = x (vô lí)
==> PT vô nghiệm

Đáp án C
Ta có: a = 2; b = - 4 nên b’ = -2 và c = m
Δ ' = ( - 2 ) 2 - 2 m = 4 - 2 m
Để phương trình đã cho vô nghiệm thì:4 – 2m < 0 hay m > 2.

a) Điều kiện xác định \(16x+8\ge0\Leftrightarrow x\ge-\frac{1}{2}.\)
Theo bất đẳng thức Cô-Si cho 4 số ta được
\(4\sqrt[4]{16x+8}=4\sqrt[4]{2\cdot2\cdot2\cdot\left(2x+1\right)}\le2+2+2+2x+1=2x+7\)
Do vậy mà \(4x^3+4x^2-5x+9\le2x+7\Leftrightarrow\left(2x-1\right)^2\left(x+2\right)\le0\).
Vì \(x\ge-\frac{1}{2}\to x+2>0\to\left(2x-1\right)^2\le0\to x=\frac{1}{2}.\)
b. Ta viết phương trình dưới dạng sau đây \(9x^4-21x^3+27x^2+16x+16=0\Leftrightarrow3x^2\left(3x^2-7x+7\right)+4\left(x+2\right)^2=0\)
Vì \(3x^2-7x+7=\frac{36x^2-2\cdot6x\cdot7+49+35}{12}=\frac{\left(6x-7\right)^2+35}{12}>0\) nên vế trái dương, suy ra phương trinh vô nghiệm.

tham khảo câu hỏi của đắng sôcôla trên hoc24.vn nha
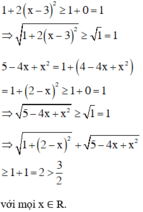
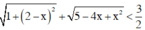 vô nghiệm.
vô nghiệm.
\(4x^2+4x+3=0\)
\(\Rightarrow\) \(4x^2+4x+1+2=0\)
\(\Rightarrow\) \(\left(2x+1\right)^2+2=0\)
\(\Rightarrow\) \(ptvn\)