Cho hàm số \(y=\dfrac{x+1}{x-1}\). Những điểm trên trục tung không kẻ được tiếp tuyến nào với đồ thị là các điểm có tung độ y thỏa mãn:
A. \(y< -1\)
B. \(y\ge-1\)
C. \(y>-1\)
D. \(y\le-1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2022
\(y'=\dfrac{-2}{\left(x-1\right)^2}\)
Gọi \(M\left(m;0\right)\) là điểm thuộc trục hoành, đường thẳng d qua M có dạng: \(y=k\left(x-m\right)\)
d không là tiếp tuyến của đồ thị khi và chỉ khi:
\(\left\{{}\begin{matrix}\dfrac{x+1}{x-1}=k\left(x-m\right)\\k=\dfrac{-2}{\left(x-1\right)^2}\end{matrix}\right.\) vô nghiệm
\(\Rightarrow\dfrac{x+1}{x-1}=\dfrac{-2\left(x-m\right)}{\left(x-1\right)^2}\) vô nghiệm
\(\Rightarrow x^2+2x-2m-1=0\) vô nghiệm
\(\Rightarrow\Delta'=2m+2< 0\Rightarrow m< -1\)
Hay \(x< -1\)
Tất cả các đáp án đều sai
AH
Akai Haruma
Giáo viên
5 tháng 4 2021
Lời giải:
$y'=\frac{-1}{(x+1)^2}$
Giao điểm của đồ thị $y=\frac{x+2}{x+1}$ vớ trục hoành là $(-2,0)$
PTTT của $y=\frac{x+2}{x+1}$ tại điểm tiếp điểm $(-2,0)$ là:
$y=f'(-2)(x+2)+f(-2)=\frac{-1}{(-2+1)^2}(x+2)+0$
$y=-x-2$
Đường tiếp tuyến $y=-x-2$ cắt trục tung tại điểm có tung độ:
$y=-0-2=-2$
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2021
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
a. \(\dfrac{2x+2}{x-1}=-2\Rightarrow2x+2=-2x+2\Rightarrow x=0\Rightarrow y'\left(0\right)=-4\)
Phương trình tiếp tuyến: \(y=-4\left(x-0\right)-2\)
b. Tiếp tuyến song song đường thẳng đã cho nên có hệ số góc k=-4
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-2\\x=2\Rightarrow y=6\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4\left(x-0\right)-2\\y=-4\left(x-2\right)+6\end{matrix}\right.\)
c. Gọi \(M\left(x_0;y_0\right)\) là tọa độ tiếp điểm
Pt tiếp tuyến qua M có dạng: \(y=\dfrac{-4}{\left(x_0-1\right)^2}\left(x-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)
Do tiếp tuyến qua A nên:
\(3=\dfrac{-4}{\left(x_0-1\right)^2}\left(4-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)
\(\Leftrightarrow x_0^2-10x_0+21=0\Rightarrow\left[{}\begin{matrix}x_0=3\Rightarrow y'\left(3\right)=-1;y\left(3\right)=4\\x_0=7;y'\left(7\right)=-\dfrac{1}{9};y\left(7\right)=\dfrac{8}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-\dfrac{1}{9}\left(x-7\right)+\dfrac{8}{3}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2021
d.
Do tiếp tuyến tạo với 2 trục tọa độ 1 tam giác vuông cân nên có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left[{}\begin{matrix}\dfrac{-4}{\left(x-1\right)^2}=1\left(vô-nghiệm\right)\\\dfrac{-4}{\left(x-1\right)^2}=-1\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=3\Rightarrow y=4\\x=-1\Rightarrow y=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-1\left(x+1\right)+0\end{matrix}\right.\)
CM
20 tháng 12 2018
Chọn A.
Tiếp điểm nằm trên trục hoành nên 
Ta có: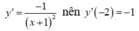 
Vậy phương tình tiếp tuyến có dạng 
Giao điểm của tiếp điểm vừa tìm với trục tung thỏa mãn hệ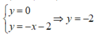 
CM
8 tháng 6 2019
Đáp án D.
y ' = 3 x 2 − 12 x + 9
Gọi M x 0 ; x 0 3 − 6 x 0 2 + 9 x 0 − 1 là một điểm bất kì thuộc (C) . Tiếp tuyến tại M:
y = 3 x 0 2 − 12 x 0 + 9 x − x 0 + x 0 3 − 6 x 0 2 + 9 x 0 − 1
⇔ y = 3 x 0 2 − 12 x 0 + 9 x − 2 x 0 3 + 6 x 0 2 − 1
Gọi A a ; a − 1 là một điểm bất kì thuộc đường thẳng y = x − 1 .
Tiếp tuyến tại M đi qua A ⇔ 3 x 0 2 − 12 x 0 + 9 a − 2 x 0 3 + 6 x 0 2 − 1 = a − 1
⇔
3
x
0
2
−
12
x
0
+
8
a
=
2
x
0
3
−
6
x
0
2
(*).
Từ A kẻ được hai tiếp tuyến đến C ⇔ * có hai nghiệm phân biệt.
Ta có
3 x 0 2 − 12 x 0 + 8 = 0 ⇔ x 0 = 6 ± 2 3 3
Dễ thấy x 0 = 6 ± 2 3 3 không thỏa mãn .
Với x 0 ≠ 6 ± 2 3 3 thì * ⇔ a = 2 x 0 3 − 6 x 0 2 3 x 0 2 − 12 x 0 + 8 .
Xét hàm số f x = 2 x 3 − 6 x 2 3 x 2 − 12 x + 8 . Ta có f ' x = 6 x 4 − 8 x 3 + 20 x 2 − 16 x 3 x 2 − 12 x + 8 2 .
Bảng biến thiên của :
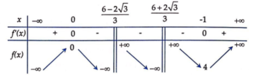
Vậy để (*) có 2 nghiệm phân biệt thì a ∈ 0 ; 4 . Suy ra tập T = 0 ; − 1 , 4 ; 3
Do đó tổng tung độ các điểm thuộc T bằng 2.
\(y'=\dfrac{-2}{\left(x-1\right)^2}\)
Gọi điểm trên trục tung có tọa độ \(M\left(0;m\right)\)
Đường thẳng d qua M có dạng: \(y=kx+m\)
d không tiếp xúc đồ thị hàm số khi và chỉ khi:
\(\left\{{}\begin{matrix}\dfrac{x+1}{x-1}=kx+m\\k=\dfrac{-2}{\left(x-1\right)^2}\end{matrix}\right.\) vô nghiệm
\(\Rightarrow\dfrac{x+1}{x-1}=\dfrac{-2x}{\left(x-1\right)^2}+m\) vô nghiệm
\(\Rightarrow\left(m-1\right)x^2-2\left(m+1\right)x+m+1=0\)
\(\Delta'=\left(m+1\right)^2-\left(m-1\right)\left(m+1\right)< 0\)
\(\Leftrightarrow2m+2< 0\)
\(\Rightarrow m< -1\)
Hay \(y< -1\)