cho tam giác ABC cân tại A . Trên tia đối tia BC lấy E , trên tia đối tia CB lấy D sao cho BE=CD
Chứng minh tam giác AED cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2023
a: Xét ΔABE và ΔACF có
AB=AC
góc ABE=góc ACF
BE=CF
Do đó: ΔABE=ΔACF
b: Xét ΔHBE vuông tại H và ΔKCF vuông tại K có
EB=FC
góc E=góc F
Do đó: ΔHBE=ΔKCF
L
13 tháng 1 2023
a) Ta có tam giác ABC cân tại A
=> Góc ABC = góc ACB
=> Góc ABE = Góc ACF ( vì góc ABE kề góc ABC, góc ACF kề góc ACB)
Xét tam giác ABE và tam giác ACF
AB = AC ( vì tam giác ABC cân tại A)
ABE = ACF ( cmt)
BE = CF (gt)
=> Tam giác ABE = Tam giác ACF (c-g-c)
=> AE = AF (hai cạnh tương ứng)
=> Tam giác AEF cân tại A
b)Ta có tam giác AEF cân tại A => góc AEB = góc AFC
Xét tam giác EBH và tam giác FCK
Góc BHE = góc CKF (=90 độ)
EB = FC (gt)
Góc HEB = Góc KFC ( vì góc AEB = góc AFC)
=> △EBH=△FCK (g-c-g)
CM
1 tháng 6 2018
Chứng minh được tam giác ABD = tam giác ACE (c-g-c) => AD = AE
Từ đó tam giác ADE cân tại A.
4 tháng 12 2022
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
PT
31 tháng 5 2017
Hình vẽ:
Giải:
Vì tam giác \(ABC\) cân tại \(A\):
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\) ( góc bù )
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB=AC \) \(\left(gt\right)\)
\(\widehat{ABD}=\widehat{ACE}\) \(\left(cmt\right)\)
\(BD=CE \) \(\left(gt\right)\)
Do đó: \(\Delta ABD=\Delta ACE\) \(\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) ( cặp cạnh tương ứng )
\(\Rightarrow\Delta ADE\) cân tại \(A\).
20 tháng 1 2018
Bài làm
Bạn tự vẽ hình nhé
Vì tam giác ABCABC cân tại A:
⇒ˆABC=ˆACB⇒ABC^=ACB^
⇒ˆABD=ˆACE⇒ABD^=ACE^ ( góc bù )
Xét ΔABDΔABD và ΔACEΔACE có:
AB=ACAB=AC (gt)
ˆABD=ˆACEABD^=ACE^ (cmt)
BD=CEBD=CE (gt)(gt)
Do đó: ΔABD=ΔACEΔABD=ΔACE (c.g.c)(c.g.c)
⇒AD=AE⇒AD=AE ( cặp cạnh tương ứng )
⇒ΔADE⇒ΔADE cân tại A
CM
7 tháng 11 2017
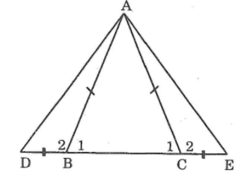
*) Ta có: ΔABC cân tại A
BD = CE (giả thiết)
Suy ra: ΔABD = ΔACE (c.g.c)
⇒ AD = AE ( hai cạnh tương ứng)
*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)
4 tháng 12 2022
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
D
11 tháng 1 2022
a, Ta có : ΔABC có AB = AC
⇒ ΔABC là tam giác cân
⇒ ∠B = ∠C = 180 - ∠A/2
Xét ΔADC và ΔAEB có :
DC = BE ( DB+BC = EC+CB )
∠ACD = ∠ABE ( chứng minh trên )
AC = AB
⇒ ΔADC = ΔAEB (c.g.c)
⇒ AD = AE ( 2 cạnh tương ứng )
b, Ta có : ∠ABD + ∠ABC = 180 ( 2 góc kề bù )
∠ACB + ∠ACE = 180 ( 2 góc kề bù )
Mà ∠ABC = ∠ACB
⇒ ∠ABD = ∠ACE
Xét ΔABD và ΔACE có :
AB = AD
∠ABD = ∠ACE
BD = CE
⇒ ΔABD = ΔACE (c.g.c)
11 tháng 1 2022
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
11 tháng 1 2022
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
