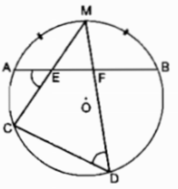
Cho nửa đường tròn đường kính AB = 2R. C là điểm chính giữa của cung AB. Trên cung AC lấy điểm F bất kỳ. Trên dây BF lấy điểm E sao cho BE = AF. Chứng minh rằng:
a. ΔAFC = ΔBEC.
b. EFC là tam giác vuông cân.
c. Gọi D là giao điểm của AC với tiép tuyến tại B của nửa đường tròn, chứng minh rằng tứ giác BECD nội tiếp


a: Xét ΔAFC và ΔBEC có
CA=CB
góc CAF=góc CBE
AF=BE
=>ΔAFC=ΔBEC
b: góc FCA=góc ECB
góc ACB=90 độ
=>góc ACE+góc BCE=90 độ
=>góc FCA+góc ACE=90 độ
=>góc FCE=90 độ
mà góc CFE=1/2*sđ cung CB=45 độ
nên ΔCFE vuông cân tại C