K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 6 2023
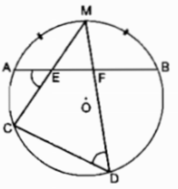
a: Xét ΔAFC và ΔBEC có
CA=CB
góc CAF=góc CBE
AF=BE
=>ΔAFC=ΔBEC
b: góc FCA=góc ECB
góc ACB=90 độ
=>góc ACE+góc BCE=90 độ
=>góc FCA+góc ACE=90 độ
=>góc FCE=90 độ
mà góc CFE=1/2*sđ cung CB=45 độ
nên ΔCFE vuông cân tại C
GN
5 tháng 6 2018
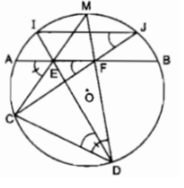
3, ta có: góc MFA = \(\frac{1}{2}\).(sđ cung AM + sđ cung BQ) (góc có đỉnh nằm trong đường tròn )
và góc MPQ = \(\frac{1}{2}\).sđ cung MQ = \(\frac{1}{2}\).. (sđ cung MB + sđ cung BQ ) (góc nội tiếp)
mà sđ cung AM = sđ cung MB (do M là điểm chính giữa cung AB )
=> góc MFA = góc MPQ
=> góc ngoài MFA tại hai đỉnh có hai góc đối nhau bằng nhau thì tứ giác EFQP là tứ giác nội tiếp hay E,F,P,Q cùng thuộc 1 đường tròn (đpcm)
