Cho hình chóp S.ABCD, SA = SB = SC. Gọi O là hình chiếu của S trên (ABC). Hỏi mệnh đề nào sau đây đúng?
A. O là trọng tâm tam giác ABC.
B. O là trực tâm tam giác ABC.
C. O là tâm đường tròn ngoại tiếp tam giác ABC.
D. O tâm đường tròn nội tiếp tam giác ABC.



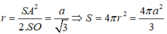
Do \(SO\perp ABC\Rightarrow\) các tam giác SOA, SOB, SOC đều vuông tại O
Đặt \(SA=SB=SC=a\) , áp dụng Pitago:
\(OA=\sqrt{SA^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OB=\sqrt{SB^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OC=\sqrt{SC^2-SO^2}=\sqrt{a^2-SO^2}\)
\(\Rightarrow OA=OB=OC\Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác ABC