Cho đường tròn (O)bán kính =2cm. Một đường thẳng đi qua điểm A nằm bên ngoài đg tròn và cắt đg tròn tại B và C trong đó AB=BC, Kẻ đg kính COD . Tính độ dài Ad
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 11 2019
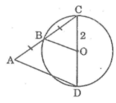
Trong tam giác ACD, ta có :
B là trung điểm của AC (gt)
O là trung điểm của CD
Nên OB là đường trung bình của ∆ACD
Suy ra : OB = (1/2).AD (tính chất đường trung bình của tam giác)
Vậy AD = 2.OB = 2.2 = 4 (cm)
24 tháng 6 2017
\(BO\) là đường trung bình của tam giác \(ACD\) nên \(BO=\dfrac{1}{2}AD\)
Do \(BO=2cm\) nên \(AD=4cm\)
13 tháng 12 2020
Sửa đề: Cho đường tròn(O) có A là điểm nằm bên ngoài đường tròn
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: OB=OC và AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA⊥BC(đpcm)
b) Xét (O) có
ΔDBC nội tiếp đường tròn có DC là đường kính
nên ΔDBC vuông tại B(Định lí)
⇒DB⊥BC
Ta có: DB⊥BC(cmt)
AO⊥BC(cmt)
Do đó: DB//AO(Định lí 1 từ vuông góc tới song song)
HS
3 tháng 4 2016
Ta có : góc AMO = góc ANO = 900 (t/c tiếp tuyến)
Mặt khác I là tđ BC => OI vuông góc BC (t/c đường kính và dây) => góc AIO = 900
=> 5 điểm A, M, O, I, N cùng nằm trên một đường tròn
Ta có góc MAI = góc MNI (AMIN nt), mà góc EBI = góc MAI (đồng vị, do AM // BE) => góc MNI = góc EBI hay góc ENI = góc EBI
=> Tứ giác NBEI nội tiếp => góc BNE = góc BIE. Mà góc BNE = góc BCM (cùng chắn cung MB trong (O))
=> góc BIE = góc BCM => IE // CM
16 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay ΔAMB cân tại M
hay \(\widehat{AMB}=60^0\)
nên ΔAMB đều
b: Xét (O) có
NA là tiếp tuyến
NC là tiếp tuyến
Do đó: ON là tia phân giác của góc AOC(1)
Xét (O) có
QC là tiếp tuyến
QB là tiếp tuyến
Do đó: OQ là tia phân giác của góc NOB(2)
Từ (1) và (2) suy ra \(\widehat{NOQ}=\dfrac{1}{2}\cdot120^0=60^0\)
8 tháng 7 2017
ai k mình k lại [ chỉ 3 người đầu tiên mà trên 10 điểm hỏi đáp ]
8 tháng 7 2017
AC.BD=\(\frac{AB^2}{4}\)<=> 4AC.BD=AB^2
<=>4AC.BD=4R^2
<=> AC.BD=R^2<=>AC.BD=AO^2 (1)
<=>áp dụng tính chất 2 tiếp tuyến cắt nhau ta có AC =CM ;BD=MD ; thế vào (1) TA đc CM.MD=AO^2
Tiếp theo ta chứng minh tam giác COD vg bằng cách dựa vào tính chất 2 tiếp tuyến cắt nhau góc MDO=MBO; MCO=MAO Mà góc MAO +ABO =90 (do tam giac AMB vuông nội tiếp chắn nửa đg tròn cóa ab là đg kính.
KHI ĐÃ CHỨNG MINH ĐƯỢC TAM GIÁC COD mà có Mo là đg cao áp dụng hệ thức lượng ta có MO ^2=CM.MDHAY AO^2=CM.MD (ĐPCM)
Trong tam giác ACD, ta có :
B là trung điểm của AC ( gt )
O là trung điểm của CD
Nên OB là đường trung bình của \(\Delta ACD\)
Suy ra : \(OB=\left(\frac{1}{2}\right).AD\) ( tính chất đường trung bình của tam giác )
Vậy AD = 2 . OB = 2 . 2 = 4 ( cm )