Nếu 0<a<b<c<d<e<f và (a-b)(c-d)(e-f) x=(b-a)(d-c)(f-e) thì x=?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu a = 0 thì (-5)a = 0;
Nếu a > 0 thì (-5)a < 0;
Nếu a < 0 thì (-5)a > 0.

a) nếu x = 3,5 thì |x| =....3,5.....
nếu x = -4/7 thì |x| =......4/7.....
b) nếu x > 0 thì |x| =......x......
nếu x = 0 thì |x| =....0...
nếu x < 0 thì |x| =...-x......
a) nếu x = 3,5 thì |x| =3,5
nếu x = -4/7 thì |x| =......4/7.....
b) nếu x > 0 thì |x| =......x......
nếu x = 0 thì |x| =....0...
nếu x > 0 thì |x| =....0......


a) Thay x = 5 vào thì phương trình trở thành \(5^2-5.5+b=0\)
\(\Rightarrow25-25+b=0\Rightarrow b=0\)
Lúc đó phương trình trở thành \(x^2-5x=0\)
\(\Leftrightarrow x\left(x-5\right)=0\)
Dễ dàng suy ra nghiệm còn lại của phương trình là 0
b) Thay x = 3 vào thì phương trình trở thành \(3^2+3b-15=0\)
\(\Rightarrow3b-6=0\Leftrightarrow b=2\)
Lúc đó phương trình trở thành \(x^2+2x-15=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+5\right)=0\)
Dễ dàng suy ra nghiệm còn lại của phương trình là -5
a) Vì \(x=5\)là 1 nghiệm của phương trình
\(\Rightarrow\)Thay \(x=5\)vào phương trình ta được:
\(5^2-5.5+b=0\)\(\Leftrightarrow25-25+b=0\)\(\Leftrightarrow b=0\)
Thay \(b=0\)vào phương trình ta được:
\(x^2-5x=0\)\(\Leftrightarrow x\left(x-5\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=5\end{cases}}\)
Vậy \(b=0\)và nghiệm thứ 2 của phương trình là \(x=0\)
b) Vì \(x=3\)là 1 nghiệm của phương trình
\(\Rightarrow\)Thay \(x=3\)vào phương trình ta được:
\(3^2+3b-15=0\)\(\Leftrightarrow9+3b-15=0\)
\(\Leftrightarrow3x-6=0\)\(\Leftrightarrow3b=6\)\(\Leftrightarrow b=2\)
Thay \(b=2\)vào phương trình ta được:
\(x^2+2x-15=0\)\(\Leftrightarrow\left(x^2-3x\right)+\left(5x-15\right)=0\)
\(\Leftrightarrow x\left(x-3\right)+5\left(x-3\right)=0\)\(\Leftrightarrow\left(x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x+5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-5\end{cases}}\)
Vậy \(b=2\)và nghiệm thứ 2 của phương trình là \(x=-5\)

\(x=\sqrt{12-\sqrt{12-\sqrt{12-...}}}\)
\(\Rightarrow x^2=12-\sqrt{12-\sqrt{12-\sqrt{12-...}}}\)
\(\Rightarrow x^2=12-x\)
\(\Rightarrow x^2+x-12=0\)
\(\Rightarrow\left(x+4\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-4< 0\left(loại\right)\\x=3\end{matrix}\right.\)
Vậy \(x=3\)

Nếu a = b và b >0 thì a = b ( *)
* Với a> 0 thì từ (*) suy ra: a= b.
⇒ 1 a - 1 b ≤ 0
* Với a < 0 từ (*) – a = b; ta có:
⇒ 1 a < 0 ; 1 b = 1 - a = - 1 a ⇒ 1 a - 1 b = 1 a - - 1 a = 2 a < 0 ( vì a < 0 )
Như vậy, ta luôn có: 1 a - 1 b ≤ 0
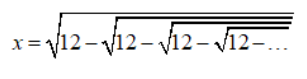 thì x bằng bn
thì x bằng bn
Vì (a-b) đối (b-a)
(c-d) đối (d-c)
(e-f) đối (f-e)
=> (a-b)(c-d)(e-f) đối (b-a)(d-c)(f-e)
=> (a-b)(c-d)(e-f).(-1)=(b-a)(d-c)(f-e)
Chúc bạn học giỏi nha!!!