Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có; x < A ⇔ - A < x < A .
Suy ra; nếu a < b thì - b < a < b ⇒ - b ≤ a ≤ b

Nếu a, b là những số thực và a ≤ b thì a 2 ≤ b 2 ⇔ a 2 ≤ b 2

Với hai số thực a, b tùy ý. Ta có: a - b ≤ a + b
Dấu “=” xảy ra khi a và b trái dấu.

Mệnh đề A đúng
Do \(x^2-x+1=\left(x-1\right)^2+\dfrac{3}{4}>0;\forall x\in R\)

\(\left\{{}\begin{matrix},m\ne0\\\Delta'>0\Leftrightarrow m^2-m>0\\x1+x2>0\Leftrightarrow2>0\\x1.x2>0\Leftrightarrow\dfrac{1}{m}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\\left[{}\begin{matrix}m< 0\\m>1\end{matrix}\right.\\m>0\\\end{matrix}\right.\)\(\Leftrightarrow m>1\)
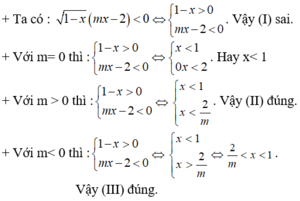
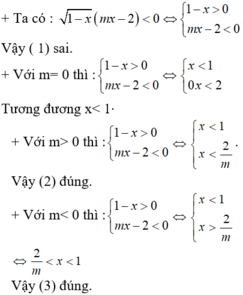
Nếu a = b và b >0 thì a = b ( *)
* Với a> 0 thì từ (*) suy ra: a= b.
⇒ 1 a - 1 b ≤ 0
* Với a < 0 từ (*) – a = b; ta có:
⇒ 1 a < 0 ; 1 b = 1 - a = - 1 a ⇒ 1 a - 1 b = 1 a - - 1 a = 2 a < 0 ( vì a < 0 )
Như vậy, ta luôn có: 1 a - 1 b ≤ 0