cho tam giác ABC có ba góc nhọn ( AB<AC). Vẽ đường cao AH, đường cao AH, đường tròn đường kính HB cắt AB tại D và đường tròn đường kính HC cắt AC tại E.
a. CMR: tứ giác ADHE nội tiếp
b. Gọi I là giao điển của DE và BC. CMR: IH^2= ID. IE
c. Gọi M,N lần lượt là giao điểm của đường thẳng DE với đường tròn đường kính HB và đtron đường kính HC. CMR: giao điểm của BM và CN nằm trên AH




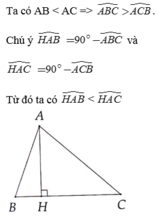

a: góc BDH=1/2*sđ cung BH=90 độ
=>HD vuông góc AB
góc HEC=1/2*sđ cung HC=90 độ
=>HE vuông góc AC
góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
b: Xét ΔIDH và ΔIHE có
góc IHD=góc IEH
góc I chung
=>ΔIDH đồng dạng với ΔIHE
=>ID/IH=IH/IE
=>IH^2=ID*IE