Cho tam giác ABC có ba góc nhọn (AB<AC), hai đường cao BD và CE cắt nhau tại H.
1. Chứng minh tam giác ABD đồng dạng tam giác ACE, từ đó suy ra AB. AE = AC.AD
2. Chứng minh tam giác ADE đồng dạng tam giác ABC
3. Gọi I là giao điểm của DE và CB và M là trung điểm của BC. Chứng minh ID.IE=IM2-MC2
4. Biết BC=15. Tính P = BH.BD + CH.CE





ĐÁP ÁN BÀI HÌNH CÂU 3, 4 ĐỀ THI TOÁN 8 KỲ 2 TINH BẮC NINH NĂM HỌC 2014-2015
3. Từ ID.IE=IM2-MC2 = ( IM - MC ) ( IM + MC ) = IB. IC ( vì MB = MC ). Xét tam giác IDB và tam giác IEC có góc I chung, góc IDB = góc ICE ( vì phụ với hai góc bằng nhau góc ADE = góc ABC theo câu 2). suy ra tam giác IBD đồng dạng tam giác IEC(g-g). suy ra ID/IC = IB/IIE => ID.IE = IB.IC hay ID.IE=IM2-MC2.(đpcm).
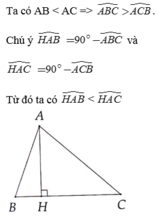
4. Hạ đường cao AH cắt BC tại K. Chứng minh được tam giác BHK đồng dạng tam giác BCD và tam giác CHK đồng dạng tam giác CBE (g-g). Suy ra BH. BD = BC. BK và CH.CE = BC. CK => P = BH.BD + CH.CE = BC ( BK+CK ) = BC. BC= BC2
Thay BC = 15 vào biểu thức ta được P = BH.BD + CH.CE = 152 = 225.
giải câu 1 với câu 2 giùm em với