Chứng minh rằng các biểu thức sau luôn dương với mọi x
a) a4 + b2 + 2 - 4ab (>= 0)
b) (x-1)(x-3)(x-4)(x-6)+9 (>=0)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1 tháng 3 2018
Bài 1) Chứng minh rằng các biểu thức sau luôn có giá trị âm với mọi giá trị của biến:
a) 9x^2+12x-15
=-(9x^2-12x+4+11)
=-[(3x-2)^2+11]
=-(3x-2)^2 - 11.
Vì (3x-2)^2 không âm với mọi x suy ra -(3x-2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -[(3*x)-2]^2-11 < 0 với mọi giá trị của x.
Hay -9*x^2 + 12*x -15 < 0 với mọi giá trị của x.
b) -5 – (x-1)*(x+2)
= -5-(x^2+x-2)
=-5- (x^2+2x.1/2 +1/4 - 1/4-2)
=-5-[(x-1/2)^2 -9/4]
=-5-(x-1/2)^2 +9/4
=-11/4 - (x-1/2)^2
Vì (x-1/2)^2 không âm với mọi x suy ra -(x-1/2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x
Do đó -11/4 - (x-1/2)^2 < 0 với mọi giá trị của x.
Hay -5 – (x-1)*(x+2) < 0 với mọi giá trị của x.
Bài 2)
a) x^4+x^2+2
Vì x^4 +x^2 lớn hơn hoặc bằng 0 vơi mọi x
suy ra x^4+x^2+2 >=2
Hay x^4+x^2+2 luôn dương với mọi x.
b) (x+3)*(x-11) + 2003
= x^2-8x-33 +2003
=x^2-8x+16b + 1954
=(x-4)^2 + 1954 >=1954
Vậy biểu thức luôn có giá trị dương với mọi giá trị của biến
A
30 tháng 6 2021
Bài 1
\(A=x^2-6x+15=x^2-2.3.x+9+6=\left(x-3\right)^2+6>0\forall x\)
\(B=4x^2+4x+7=\left(2x\right)^2+2.2.x+1+6=\left(2x+1\right)^2+6>0\forall x\)
Bài 2
\(A=-9x^2+6x-2021=-\left(9x^2-6x+2021\right)=-\left[\left(3x-1\right)^2+2020\right]=-\left(3x-1\right)^2-2020< 0\forall x\)
CM
5 tháng 7 2018
Điều kiện x ≠ 1 và x ≠ - 1
Ta có:
Biểu thức dương khi x 2 + 2 x + 3 > 0
Ta có: x 2 + 2 x + 3 = x 2 + 2 x + 1 + 2 = x + 1 2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1
CM
10 tháng 7 2018
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
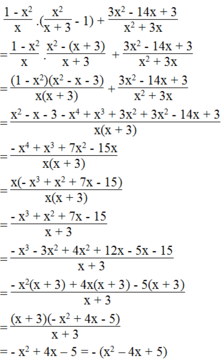
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
KN
2 tháng 8 2019
a) \(x^2+x+1=x^2+x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)
KN
2 tháng 8 2019
c) \(C=4x-10-x^2=-\left(x^2-4x+10\right)\)
\(=-\left(x^2-4x+4+6\right)=-\left[\left(x-2\right)^2+6\right]\)
\(=-\left(x^2-4x+4+6\right)=-\left[\left(x-2\right)^2\right]-6\le-6< 0\forall x\)
19 tháng 8 2020
+) \(A=x\left(x-6\right)+10\)
\(A=x^2-6x+10\)
\(A=x^2-6x+9+1\)
\(A=\left(x-3\right)^2+1\ge1\)
Vậy.....
+) \(B=x^2-2x+9y^2-6y+3\)
\(B=\left(x^2-2x+1\right)+\left(9y^2-6y+1\right)+1\)
\(B=\left(x-1\right)^2+\left(3y-1\right)^2+1\ge1\)
Vậy .....
DM
0
b
= (x2-7x+6)(x2-7x+12)+9
đặt x2-7x+9=a ta đc
(a-3)(a+3)+9=a2-32+9=a2 >= 0 với mọi x ( đpcm)
Chứng minh rằng các biểu thức sau luôn dương với mọi x
a) a4 + b2 + 2 - 4ab (>= 0)
b) (x-1)(x-3)(x-4)(x-6)+9 (>=0)
= (x2-7x+6)(x2-7x+12)+9
đặt x2-7x+9=a ta đc
(a-3)(a+3)+9=a2-32+9=a2 >= 0 với mọi x ( đpcm)