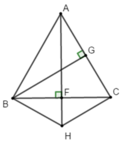
Cho tam giác ABC đều.Từ A kẻ AF vuông góc BC tại F,từ B kẻ BG vuông góc AC tại G.Qua C kẻ đường thẳng song song với BG cắt AF tại H. Khi đó tam giá HBC là
A.tam giác đều B.tam giác vuông C.tam giác vuông cân D.tam giác cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
19 tháng 2 2021
\(\Delta\)ABC cân, mà AF là đường cao
=> AF là đường trung tuyến ( định lý )
=> BF=CF
Xét \(\Delta\) BFH và \(\Delta\) CFH có: \(\left\{{}\begin{matrix}BF=CF\\F_1=F_2=90^o\\FH\end{matrix}\right.\)
=> \(\Delta\) BFH = \(\Delta\) CFH (c.g.c)
=> BH=CH ( 2 cạnh tương ứng )
=> \(\Delta\) BHC là tam giác cân ( định lý )
CM
27 tháng 5 2019
+ Xét tam giác ABF và tam giác ACF đều vuông tại F có:
AB = AC (tam giác ABC đều)
AF: cạnh chung
Do đó: Δ A B F = Δ A C F (cạnh huyền – cạnh góc vuông)
Suy ra: BF = CF (hai cạnh tương ứng)
+ Xét hai tam giác BFH và CFH cùng vuông tại F có:
FH cạnh chung
BF = CF (cmt)
Do đó: Δ B F H = Δ C F H (hai cạnh góc vuông)
Suy ra: CH = BH (hai cạnh tương ứng)
⇒ Δ H B C cân tại H
+ Ta có: B C G ^ + G B C ^ = 90 ° (tam giác BCG vuông tại G)
Mà B C G ^ = B C A ^ = 60 ° (tam giác ABC đều)
Nên G B C ^ = 90 ° − B C G ^ = 90 ° − 60 ° = 30 °
+ Lại có: BG // CH (gt) ⇒ H C B ^ = G B C ^ = 30 ° (hai góc so le trong)
Tam giác HBC cân tại H có góc ở đáy H C B ^ = 30 ° nên Δ H B C không thể là tam giác vuông cân và tam giác đều.
Vậy A, B, C sai, D đúng
Chọn đáp án D
8 tháng 4 2022
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
Do đó: ΔAEB\(\sim\)ΔAFC
Suy ra: AE/AF=AB/AC
hay \(AE\cdot AC=AB\cdot AF\)
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc EAF chung
Do đó: ΔAEF\(\sim\)ΔABC
Suy ra: \(\widehat{AEF}=\widehat{ABC}\)
N
15 tháng 12 2019
Bạn có thể tự vẽ hình chứ ? Tại hình hơi rối nên mình lười vẽ =)))
a) Xét ∆ABD và ∆CED có :
DA = DC (D là trung điểm của AC)
∠ADB = ∠CDE (2 góc đối đỉnh)
DB = DE (GT)
=> ∆ABD = ∆CED (c.g.c)
=> ∠ABD = ∠CED (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> AB // CE (DHNB)
b) Ta có : AF ⊥ BD (GT)
Mà CG ⊥ DE (GT)
=> AF // CG (Tính chất)
=> ∠DAF = ∠DCG (2 góc so le trong) (1)
Xét ∆ADF và ∆CDG có :
∠DAF = ∠DCG (Theo (1))
DA = DC (D là trung điểm của AC)
∠ADF = ∠CDG (2 góc đối đỉnh)
=> ∆ADF = ∆CDG (g.c.g)
=> DF = DG (2 cạnh tương ứng)
c) Mình cũng có chứng minh thẳng hàng mấy lần rồi nhưng nhìn hình thì mình không tìm được các yếu tố có thể chứng minh nên bạn nhờ ai khác nhé.
