GIÚP EM VỚI Ạ E CẢM ƠNN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giúp e với ạ e cảm ơnn
7 tháng 8 2021
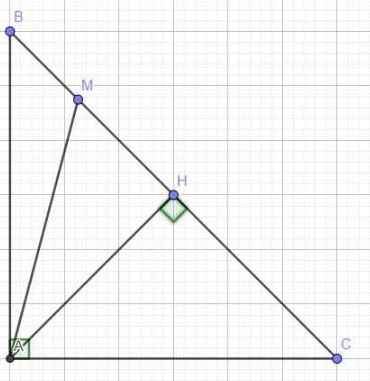
a)Kẻ AH⊥BC
Vì ΔABC vuông cân tại A
⇒ AH cũng là đường trung tuyến
⇒ AH=BH=CH
Ta có:MB2 + MC2 = (BH-HM)2 + (CH+HM)2 = (AH-HM)2+(AH+HM)2
= AH2-2.AH.HM+HM2+AH2+2.AH.HM+HM2=2(AH2+HM2)
Áp dụng định lý Py-ta-go vào ΔAHM vuông tại A ta có:
MA2 = AH2+HM2
⇒ MB2+MC2=2MA2
b) Ta có: MA≥AH (đường xiên và đường vuông góc)
⇒ MA2 ≥ AH2
⇒ 2MA2 ≥ 2AH2
⇒ MB2+MC2 ≥ 2AH2
Dấu "=" xảy ra ⇔ MA=AH ⇔ M là trung điểm của BC
Vậy Min K = 2AH2 ⇔ M là trung điểm của BC
NT
1
27 tháng 2 2023
1: Khi x=3-2 căn 2 thì \(A=\dfrac{\sqrt{2}-1+2}{\sqrt{2}-1}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}=3+2\sqrt{2}\)
2: \(B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}=\dfrac{x+2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
3: \(P=A:B=\dfrac{\sqrt{x}+2}{\sqrt{x}}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{x-4}{x}\)
\(x\cdot P< =10\sqrt{x}-29-\sqrt{x-25}\)
=>\(x-4< =10\sqrt{x}-29-\sqrt{x-25}\)
\(\Leftrightarrow x-4-10\sqrt{x}+29< =-\sqrt{x-25}\)
=>\(x-10\sqrt{x}+25< =-\sqrt{x-25}\)
=>(căn x-5)^2<=-căn x-25
=>x-25=0
=>x=25
