cho tam giac1abc vuộng tại a,biết ab=6cm,ac=8cm.tính bc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LA
3
5 tháng 3 2022
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{10}=\dfrac{24}{5}cm\)
* Áp dụng hệ thức \(AB^2=HB.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)
\(CH=BC-BH=10-\dfrac{18}{5}=\dfrac{32}{5}cm\)
20 tháng 2 2015
bài này ko đủ dữ kiện. nếu bổ sung dữ kiện thì ta có thể tính dc với cách tính của định lý pitago.những bài này thường có 3 dữ kiện trở lên
AT
18 tháng 7 2021
a) tam giác ABC vuông tại A nên áp dụng Py-ta-go:
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4.8\left(cm\right)\)
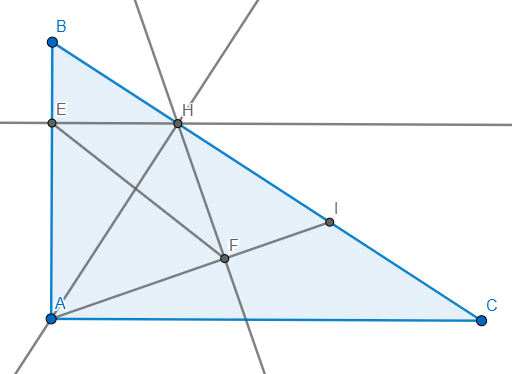
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHI vuông tại H có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AI=AH^2\Rightarrow AF.AI=AE.AB\Rightarrow\dfrac{AF}{AB}=\dfrac{AE}{AI}\)
Xét \(\Delta AEF\) và \(\Delta AIB:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AE}{AI}=\dfrac{AF}{AB}\\\angle BAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta AIB\left(c-g-c\right)\)
18 tháng 7 2021
1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
23 tháng 6 2023
a: \(AB=\sqrt{6^2+8^2}=10\left(cm\right)\)
BH<AH<AB
=>góc HAB<góc HBA<góc AHB
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
c: góc KAH=góc HAC
góc KHA=góc HAC
=>góc KAH=góc KHA
=>ΔAKH cân tại K
Xét ΔABC có
H là trung điểm của BC
HK//AC
=>K là trung điểm của AB
21 tháng 10 2022
Bài 2:
góc ACB=90-30=60 độ
Xét ΔABC vuông tại A có sin ABC=AC/BC
nên AC/BC=1/2
=>AC=4cm
=>\(AB=4\sqrt{3}\left(cm\right)\)
23 tháng 12 2020
Theo định lý Pytago ta tính được BC = 10cm
Vì tam giác ABC vuông tại A nên ta có:
+) sinB = \(\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
+) tanC = \(\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\)
=> sinB + tanC= \(\dfrac{4}{5}+\dfrac{3}{4}=\dfrac{31}{20}\)
DQ
3
5 tháng 1 2022
Áp dụng định lý Pytago vào ΔABC vuông tại A ta có:
\(BC^2=AB^2+AC^2=6^2+8^2\Leftrightarrow BC=10\left(cm\right)\)
\(\Rightarrow sinC=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
10
Xét \(\Delta ABC\) vuông tại \(A\) có:
\(BC^2=AB^2+AC^2\) (đ/l Pytago)
\(\Rightarrow BC=\sqrt{6^2+8^2}\)
\(\Rightarrow BC=10cm\)