Em xin lời giải ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Người ta có cho hàm f(x) là gì hay tích phân của hàm f(x) bằng bao nhiêu ko ?

Có: \(I=\int\limits^{ln3}_0\sqrt{e^x-1}e^xdx\)
Đặt \(t=\sqrt{e^x-1}\Rightarrow t^2=e^x-1\)
\(\Rightarrow2tdt=e^xdx\)
\(\Rightarrow I=\int\limits^{\sqrt{2}}_02t^2dt\) \(\Rightarrow I=\dfrac{2}{3}t^3|^{\sqrt{2}}_0=\dfrac{4}{3}\sqrt{2}\)
Vậy a=0, b=\(\dfrac{4}{3}\) \(\Rightarrow a+b=0+\dfrac{4}{3}=\dfrac{4}{3}\)

a)Động năng tại \(v_0=0\)m/s:
\(W_{đ1}=\dfrac{1}{2}mv_0^2=0J\)
Động năng tại \(v=200\)cm/s=2m/s:
\(W_{đ2}=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot1\cdot2^2=2J\)
b)Độ biến thiên động năng:
\(\Delta W=W_{đ2}-W_{đ1}=2-0=2J\)
c)Công lực kéo chính là độ biến thiên động năng:
\(A_k=\Delta W=2J\)
d)Lực kéo có độ lớn:
\(F_k=\dfrac{A_k}{s}=\dfrac{2}{2}=1N\)

Câu 2.
Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot m\cdot6^2+m\cdot10\cdot0=18m\left(J\right)\)
a)Cơ năng tại nơi có độ cao cực đại:
\(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\Rightarrow h_{max}=\dfrac{18}{10}=1,8m\)
b)Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\Rightarrow z=\dfrac{18}{2g}=\dfrac{18}{2\cdot10}=0,9m\)
c)Cơ năng tại nơi \(W_đ=2W_t\):
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{18}{3\cdot10}=0,6m\)

giải nghĩa:
lễ vật: vật dùng để biếu tặng hoặc cúng tế
đây là cách giải nghĩa nêu lên khái niệm nội dung mà từ biểu thị
Trong vb này phải dùng từ"sính lễ"mới chuẩn xác
Vì:sính lễ: lễ vật của nhà trai đem đến nhà gái để xin cưới
Nên dùng từ "sính lễ"vì làm vậy sẽ rõ ràng và hợp với ngữ cảnh trong văn bản


\(\int\limits^2_1\dfrac{2x+1}{x^2+x}dx=\int\limits^2_1\dfrac{d\left(x^2+x\right)}{x^2+x}=ln\left(x^2+x\right)|^2_1=ln6-ln2=ln3\)
\(\Rightarrow\left\{{}\begin{matrix}a=0\\b=3\end{matrix}\right.\) \(\Rightarrow a^2+b^2=9\)






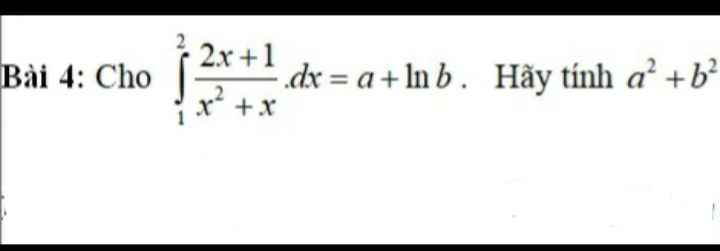
Đặt \(z=x+yi\)
\(\dfrac{\left(x+yi\right)\left(1+i\right)}{2}+\left(x-yi\right)\left(5+2i\right)=31-17i\)
\(\Leftrightarrow x-y+\left(x+y\right)i+10x+4xi-10yi+4y=31-17i\)
\(\Leftrightarrow\left(11x+3y\right)+\left(5x-9y\right)i=62-34i\)
\(\Leftrightarrow\left\{{}\begin{matrix}11x+3y=62\\5x-9y=-34\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)