
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đặt \(z=x+yi\)
\(\dfrac{\left(x+yi\right)\left(1+i\right)}{2}+\left(x-yi\right)\left(5+2i\right)=31-17i\)
\(\Leftrightarrow x-y+\left(x+y\right)i+10x+4xi-10yi+4y=31-17i\)
\(\Leftrightarrow\left(11x+3y\right)+\left(5x-9y\right)i=62-34i\)
\(\Leftrightarrow\left\{{}\begin{matrix}11x+3y=62\\5x-9y=-34\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)

Có: \(I=\int\limits^{ln3}_0\sqrt{e^x-1}e^xdx\)
Đặt \(t=\sqrt{e^x-1}\Rightarrow t^2=e^x-1\)
\(\Rightarrow2tdt=e^xdx\)
\(\Rightarrow I=\int\limits^{\sqrt{2}}_02t^2dt\) \(\Rightarrow I=\dfrac{2}{3}t^3|^{\sqrt{2}}_0=\dfrac{4}{3}\sqrt{2}\)
Vậy a=0, b=\(\dfrac{4}{3}\) \(\Rightarrow a+b=0+\dfrac{4}{3}=\dfrac{4}{3}\)

\(z=x+yi\Rightarrow w=\dfrac{z}{2+i}=\dfrac{x+yi}{2+i}=\dfrac{\left(x+yi\right)\left(2-i\right)}{4-i^2}=\dfrac{2x+y}{5}+\dfrac{2y-x}{5}i\)
\(\left(1+3i\right)w+1+7i=\left(1+3i\right)\left(\dfrac{2x+y}{5}+\dfrac{2y-x}{5}i\right)+1+7i\)
\(=x-y+1+\left(x+y+7\right)i\)
\(\Rightarrow\left(x-y+1\right)^2+\left(x+y+7\right)^2=50\)
\(\Leftrightarrow x^2+y^2+8x+6y=0\)
Tập hợp z là đường tròn tâm \(I\left(-4;-3\right)\) bán kính \(R=5\)

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)

1b/ \(\overrightarrow{AB}=\left(1;1;3\right);\overrightarrow{u_{Oy}}=\left(0;1;0\right)\)
Vì \(\left(P_2\right)//AB//Oy\Rightarrow\overrightarrow{n_{\left(P_2\right)}}=\left[\overrightarrow{AB},\overrightarrow{u_{Oy}}\right]=\left(\left|\begin{matrix}1&3\\1&0\end{matrix}\right|,\left|\begin{matrix}3&1\\0&0\end{matrix}\right|,\left|\begin{matrix}1&1\\0&1\end{matrix}\right|\right)=\left(-3;0;1\right)\)
\(\Rightarrow\left(P_2\right):-3\left(x+3\right)+z-5=0\Leftrightarrow\left(P_2\right):3x-z+14=0\)
2b/
\(\overrightarrow{u_{Ox}}=\left(1;0;0\right);\overrightarrow{n_{\left(Q\right)}}=\left(3;2;5\right)\)
\(\Rightarrow\overrightarrow{n_{\left(\beta\right)}}=\left[\overrightarrow{u_{Ox}},\overrightarrow{n_{\left(Q\right)}}\right]=\left(0;-5;2\right)\)
\(d\left(O,\left(\beta\right)\right)=\dfrac{\left|d\right|}{\sqrt{25+4}}=\sqrt{29}\Rightarrow d=\pm29\)
\(\Rightarrow\left[{}\begin{matrix}\left(\beta\right):-5y+2z+29=0\\\left(\beta\right):-5y+2z-29=0\end{matrix}\right.\)
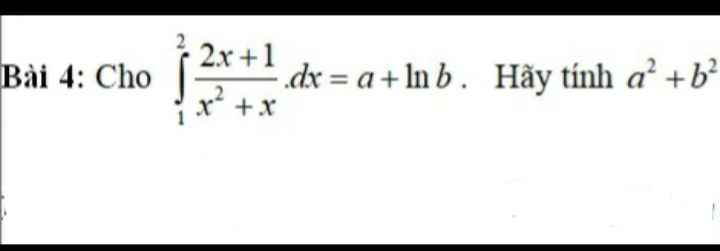
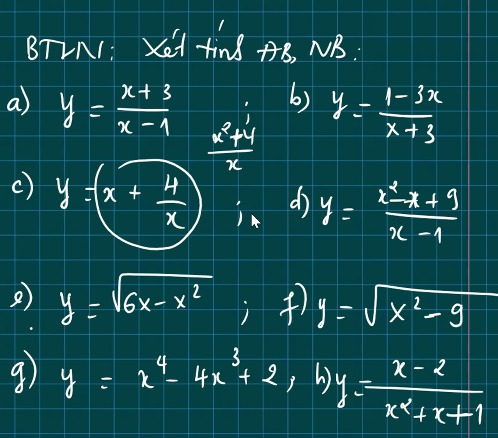 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ




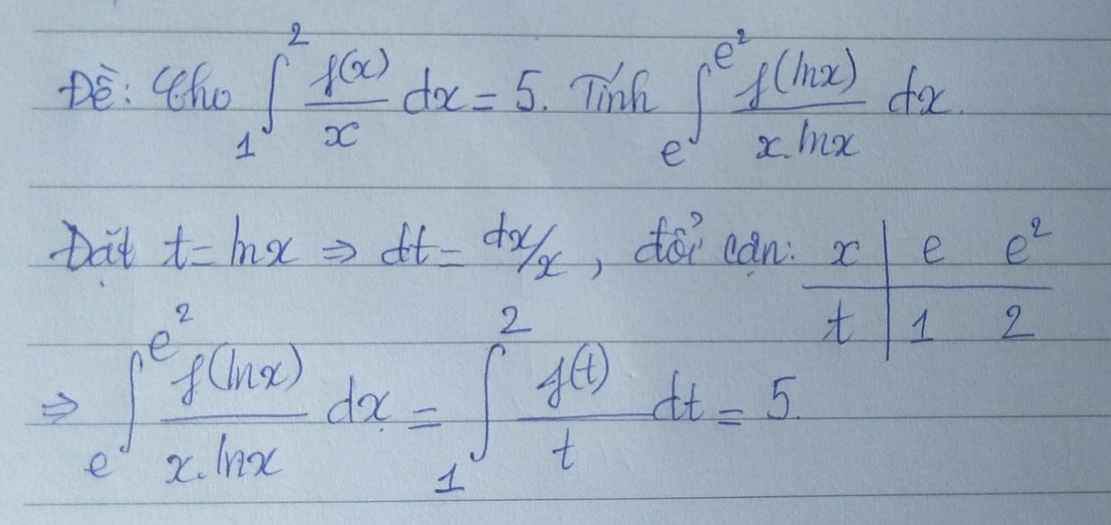



\(\int\limits^2_1\dfrac{2x+1}{x^2+x}dx=\int\limits^2_1\dfrac{d\left(x^2+x\right)}{x^2+x}=ln\left(x^2+x\right)|^2_1=ln6-ln2=ln3\)
\(\Rightarrow\left\{{}\begin{matrix}a=0\\b=3\end{matrix}\right.\) \(\Rightarrow a^2+b^2=9\)