Chứng minh các đẳng thức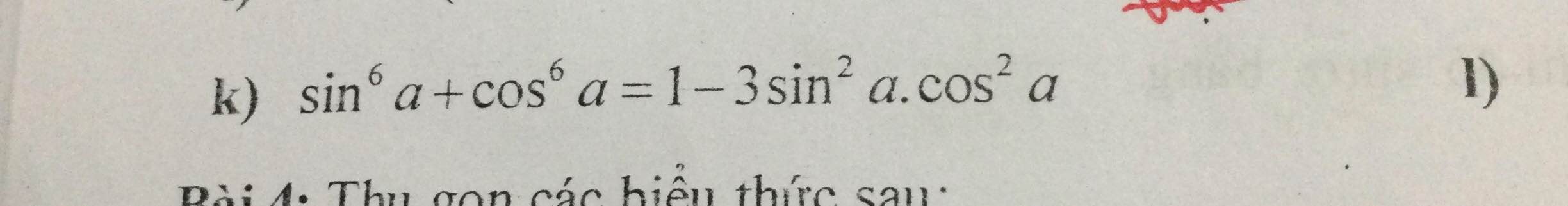
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
18 tháng 7 2021
b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(-\sqrt{7}-\sqrt{5}\right).\left(\sqrt{7}-\sqrt{5}\right)=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
\(=-\left(7-5\right)=-2\)
c) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)=a-b\)
d) \(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)
CP
18 tháng 7 2021
b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(-\sqrt{7}+\left(-\sqrt{5}\right)\right).\left(\sqrt{7}-\sqrt{5}\right)=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)=-2\)
CM
26 tháng 6 2018
a) Ta có: x5 – 1 = (x – 1)(x4 + x3 + x2 + x + 1)
Lại có: x – 1 > 0 ⇒ x > 1 ⇒ x5 > x4 > x3 > x2 > x > 1
⇒ 1 + 1 + 1 + 1 + 1 < x4 + x3 + x2 + x + 1 < x4 + x4 + x4 + x4 + x4
hay 5 < x4 + x3 + x2 + x + 1 < 5x4
⇒ 5.(x – 1) < (x – 1)(x4 + x3 + x2 + x + 1) < 5x4.(x – 1)
hay 5.(x – 1) < x5 – 1 < 5x4.(x – 1) (đpcm)
b) x5 + y5 – x4y – xy4 = (x5 - x4y) - (xy4 - y5)
= x4.(x – y) – y4.(x – y)
= (x4 – y4).(x – y)
= (x2 + y2)(x2 – y2)(x – y)
= (x2 + y2).(x + y)(x – y)(x – y)
= (x2 + y2)(x + y)(x – y)2
Mà x2 + y2 ≥ 0; x + y ≥ 0; (x – y)2 ≥ 0
⇒ x5 + y5 – x4y – xy4 ≥ 0.
c) Ta có: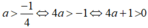 
Tương tự. 4b +1 >0 và 4c +1 > 0
Áp dụng bất đẳng thức Cô-si cho hai số dương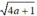 
và 1 ta có:
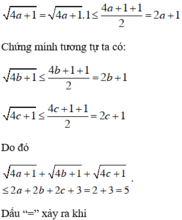
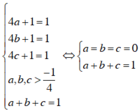
Không có giá trị nào của a, b, c thỏa mãn hệ trên nên dấu “=” của BĐT không xảy ra.
PT
1
CM
14 tháng 1 2018
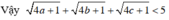
7520 = 4510.530
Ta có: 4510.530 = (9.5)10.530 = 910.510.530 = (32)10.540
=320.(52)20 = 320.2520 = (3.25)20 = 7520
Vế phải bằng vế trái nên đẳng thức được chứng minh
CM
9 tháng 11 2017
128.912 = 1816
Ta có: 128.912 = (4.3)8.912 =48.38.912 =(22)8.(32)4.912
= 216.94.912 = 216.916= (2.9)16 = 1816
Vế trái bằng vế phải nên đẳng thức được chứng minh
PT
1
CM
26 tháng 3 2018
cosα = OH¯; sinα = OK¯
Do tam giác OMK vuông tại K nên:
sin2 α + cos2 α = OK¯2 + OH¯2 = OK2 + MK2 = OM2 = 1.
Vậy sin2 α + cos2 α = 1.
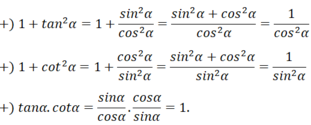
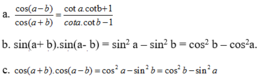
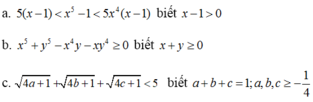
\(sin^6a+cos^6a=\left(sin^2a\right)^3+\left(cos^2a\right)^3\)
\(=\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)\)
\(=1-3sin^2a.cos^2a\)