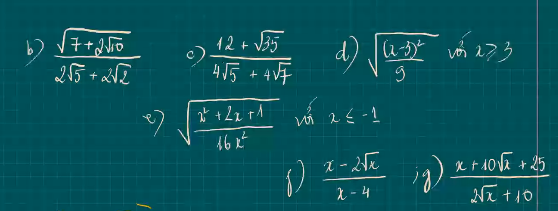Làm hộ em ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=A.B=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}.\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\)
\(=1+\dfrac{9}{\sqrt{x}-3}\le1+\dfrac{9}{0-3}=1-3=-2\)
\(maxP=-2\Leftrightarrow x=0\)
\(1,x=16\Leftrightarrow A=\dfrac{4-1}{4-3}=\dfrac{3}{1}=3\\ 2,B=\dfrac{x+2\sqrt{x}-3+5\sqrt{x}+5+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\\ 3,P=AB=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\\ P=1+\dfrac{9}{\sqrt{x}-3}\\ Vì.\sqrt{x}-3\ge-3\Leftrightarrow\dfrac{9}{\sqrt{x}-3}\le-3\\ \Leftrightarrow P=1+\dfrac{9}{\sqrt{x}-3}\le1-3=-2\\ P_{max}=-2\Leftrightarrow x=0\)

1 is going
2 enjoy
3 seem
4 feel
5 are learning
6 needs
7 concentrate
8 support
9 is doing
10 are practicing
11 finds
12 is getting
13 think
1. goes
2. enjoy
3. seem
4. feel
5. are learning
6. needs
7. concentrate
8. support
9. does
10. are practicing
11. finds
12. gets
13. think

Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm

\(a,\dfrac{6.12-6.7}{60}=\dfrac{6\left(12-7\right)}{60}=\dfrac{6.5}{60}=\dfrac{30}{60}=\dfrac{1}{2}\\ b,\dfrac{35.18-35}{\left(-34\right).7}=\dfrac{35\left(18-1\right)}{\left(-34\right).7}=\dfrac{35.17}{\left(-34\right).7}=\dfrac{595}{-238}=\dfrac{-5}{2}\)
\(c,\dfrac{42-11.42}{21.\left(-15\right)}=\dfrac{42\left(1-11\right)}{21.\left(-15\right)}=\dfrac{2.21.\left(-10\right)}{21.\left(-15\right)}=\dfrac{-20}{-15}=\dfrac{4}{3}\)

Câu 1:
-Phương thức biểu đạt chính: tự sự.
Câu 2:
-Nội dung chính của văn bản: Văn bản trên kể về câu chuyện của chàng trai Nguyễn Văn Nhã đã dũng cảm cứu ba bạn nữ bị đuối nước. Qua đó, ca ngợi lòng gan dạ, dũng cảm, quên mình xả thân cứu người gặp nạn.
Câu 3:
- Phép tu từ nổi bật trong câu văn là phép điệp từ "một...".
-Hiệu quả: Điệp từ "một" điệp lại ba lần trong câu văn tạo điểm nhấn mạnh mẽ, thể hiện sự trân trọng đức hi sinh cao cả của Nguyễn Văn Nhã, điệp từ còn gây ấn tượng cho người đọc và tạo nhịp điệu cho câu văn.
Câu 4:
-Sự hi sinh của Nguyễn Văn Nhã gợi cho tôi nhiều sự xúc động và thật đáng trân trọng. Dù đã là sinh viên năm 4 đứng trước nhiều cơ hội sự nghiệp cho tương lai, thế nhưng khi thấy người gặp nguy, anh đã không còn nghĩ đến cái "tôi" cá nhân của mình. "Một mạng ra đi có thể đổi lại ba mạng sống", vâng! Giữa ranh giới của sự sống còn, anh đã đấu tranh bằng mạng sống với tử thần để cứu lấy ba cô bạn xui rủi. Hành động ấy đã nêu cao tinh thần dũng cảm, quên mình đáng trân trọng của anh. Tuy anh đã ra đi, để lại bao xót xa, ngậm ngùi cho những người thân ở lại, nhưng gương sáng Nguyễn Văn Nhã vẫn luôn sống trong tim người.



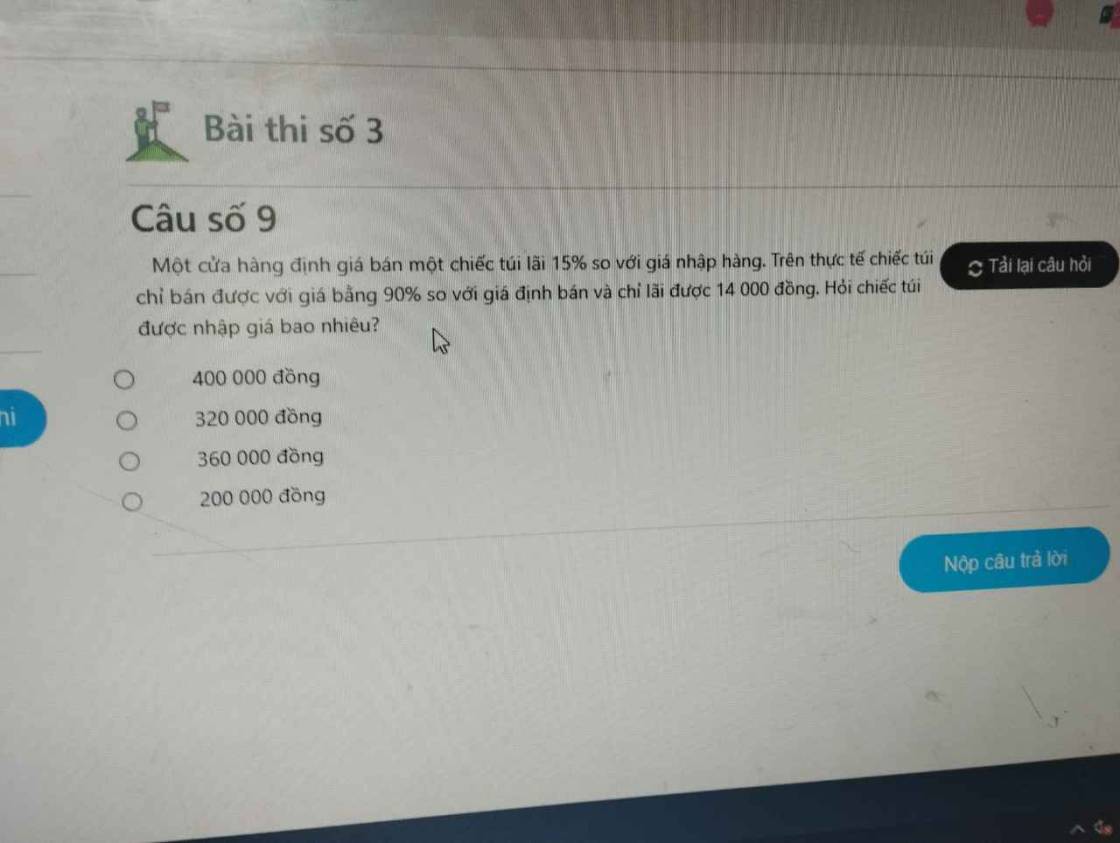
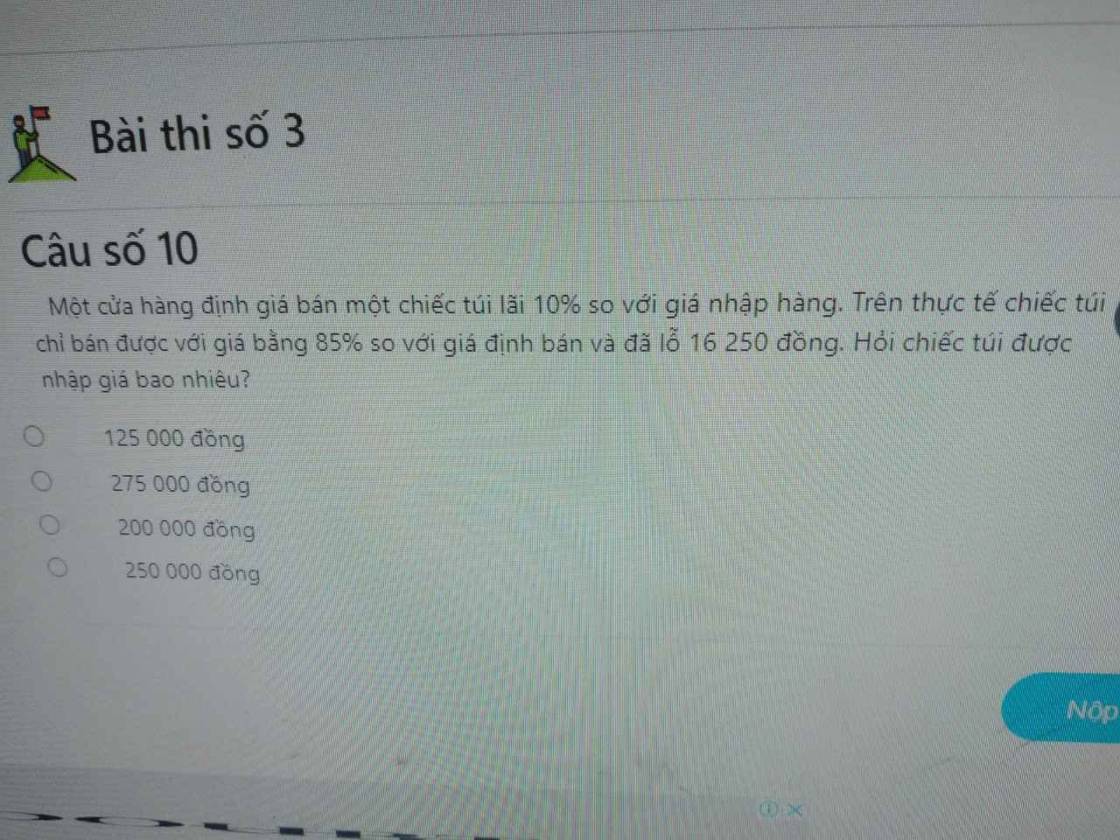


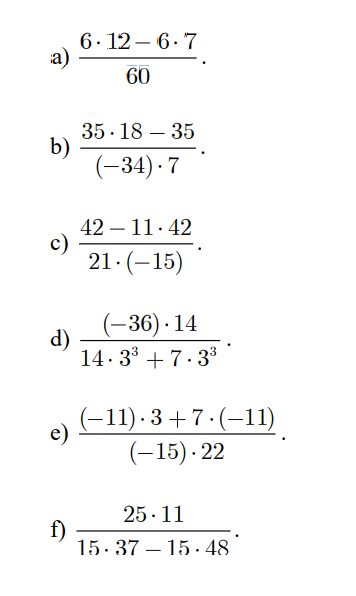 làm hộ em với ạ em đg gấp
làm hộ em với ạ em đg gấp 
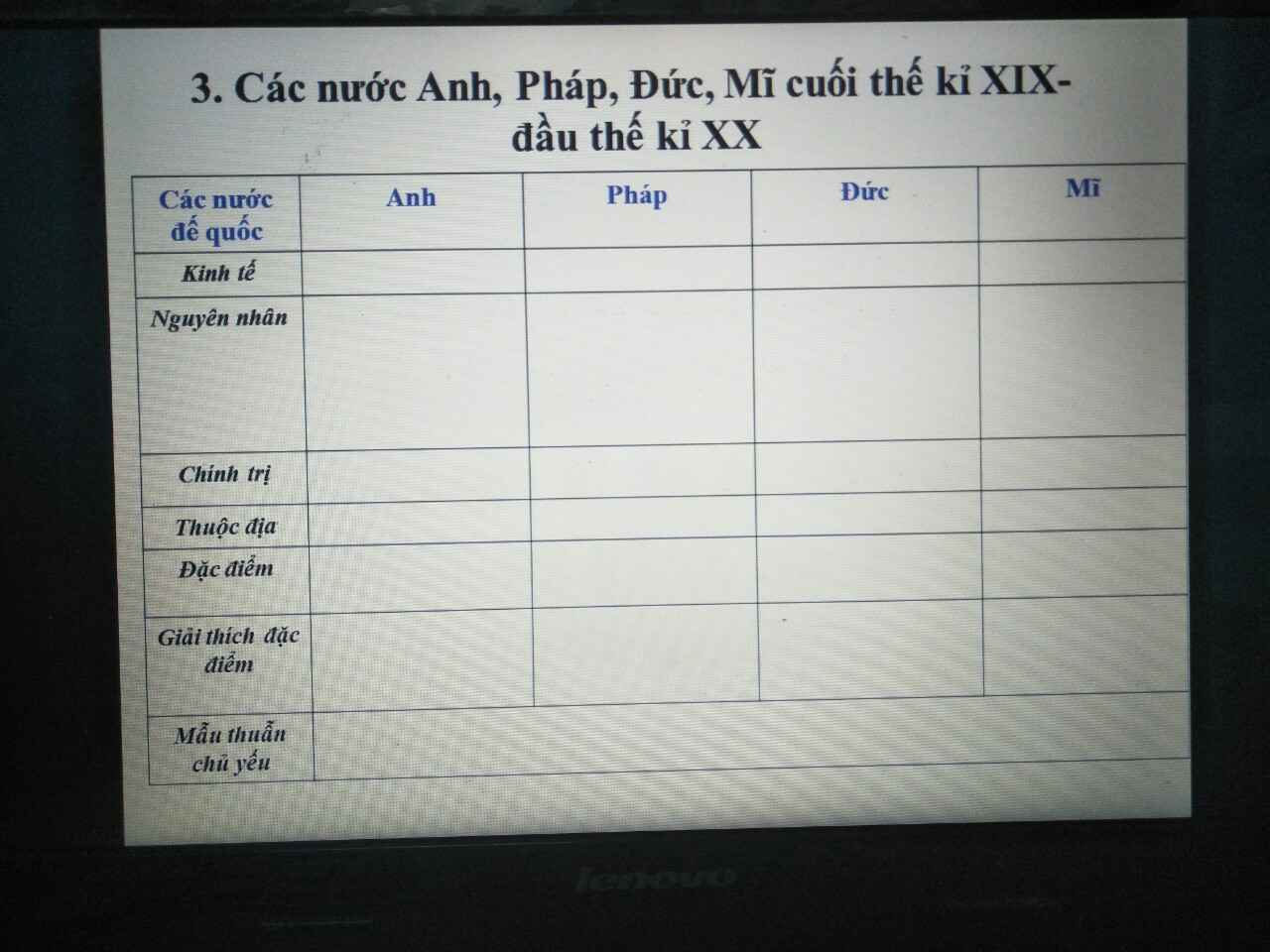 Ai làm hộ em với ạ e cần gấp ạ
Ai làm hộ em với ạ e cần gấp ạ