Mọi người làm giúp mình bài 1,2 nha. Mình cảm ơn mn người rất nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MD
1
Những câu hỏi liên quan
BC
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
7
AH
Akai Haruma
Giáo viên
17 tháng 2 2021
Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$
NV
5
12 tháng 4 2021
4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).
Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Rightarrow xy+yz+zx=-1\).
Bất đẳng thức đã cho tương đương:
\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).
Vậy ta có đpcm
12 tháng 4 2021
mình xí câu 45,47,51 :>
45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)
Đẳng thức xảy ra <=> a=b
b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)
\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)
\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)
Cộng (1),(2),(3) theo vế ta có đpcm
Đẳng thức xảy ra <=> a=b=c
ND
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 3 2023
em ơi chưa có bài em nhé, em chưa tải bài lên lám sao mình giúp được
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
14 tháng 12 2021
\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
14 tháng 12 2021
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...
H
1
25 tháng 6 2021
uses crt;
var a:array[1..1000]of integer;
n,i,k,min,vt:integer;
begin
clrscr;
write('Nhap n='); readln(n);
if n=0 then writeln('Moi ban nhap lai')
else begin
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(a[i]:4);
writeln;
min:=a[1];
vt:=1;
for i:=1 to n do
if min>a[i] then
begin
min:=a[i];
vt:=i;
end;
writeln('So nho nhat la: ',min,' tai vi tri: ',vt);
write('Nhap k='); readln(k);
for i:=1 to n do
if i<>k then write(a[i]:4);
end;
readln;
end.
1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
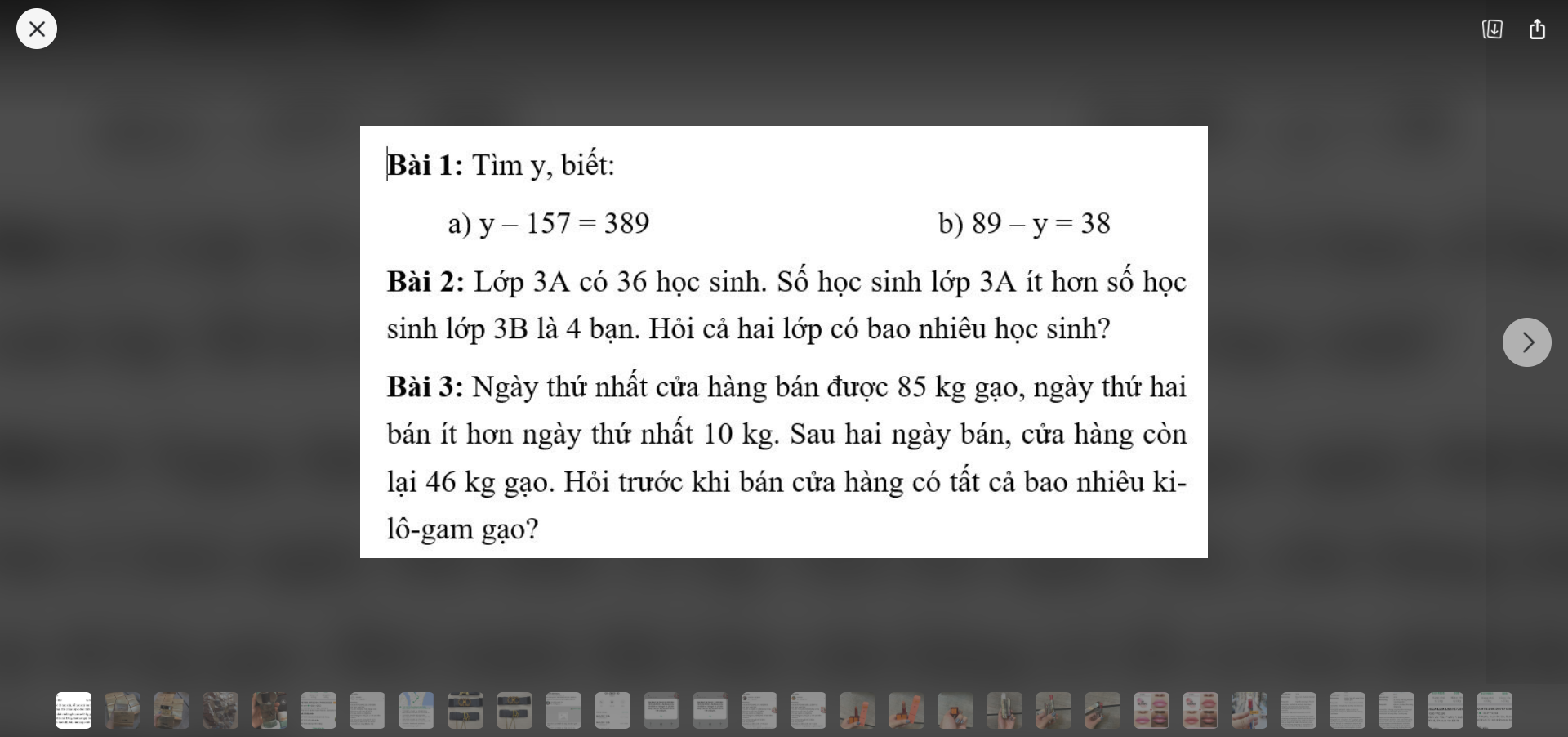
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác vuông
• Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )
• Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )
• Cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)
• Cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :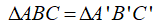
2. Các trường hợp bằng nhau của tam giác
a. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Xét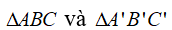
có:
AB = A’B’
AC = A’C’
BC = B’C’
thì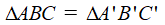
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau
c. Trường hợp bằng nhau thứ ba của hai tam giác: góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
tik cho mình nha mình đc câu1 nè