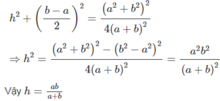Một hình chóp lục giác đều có diện tích xung quanh bằng hai lần diện thích đáy
a) tính góc tạo bởi trung đoạn và đường cao của hình chóp
b) Diện tích xung quanh hình chóp là bao nhiêu biết diện tích đáy bằng 2cm2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
J
28 tháng 5 2021
Trong các khẳng định dưới đây, khẳng định nào đúng?
| Trung đoạn của hình chóp đều là đường cao hạ từ đỉnh xuống mặt phẳng đáy. SAI | ||
| Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và hai lần diện tích đáy. SAI | ||
| Diện tích xung quanh của hình chóp bằng tích của nửa chu vi đáy và trung đoạn. ĐÚNG |
CM
25 tháng 6 2019
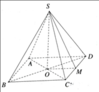
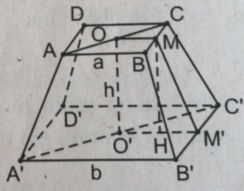
Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
S x q = 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′=
a
2
+
b
2
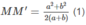
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
Trong tam giác vuông MHM' ta có: M M ' 2 = M H 2 + H M ' 2 = h + b - a / 2 2 (2)
Từ (1) và (2) suy ra :
