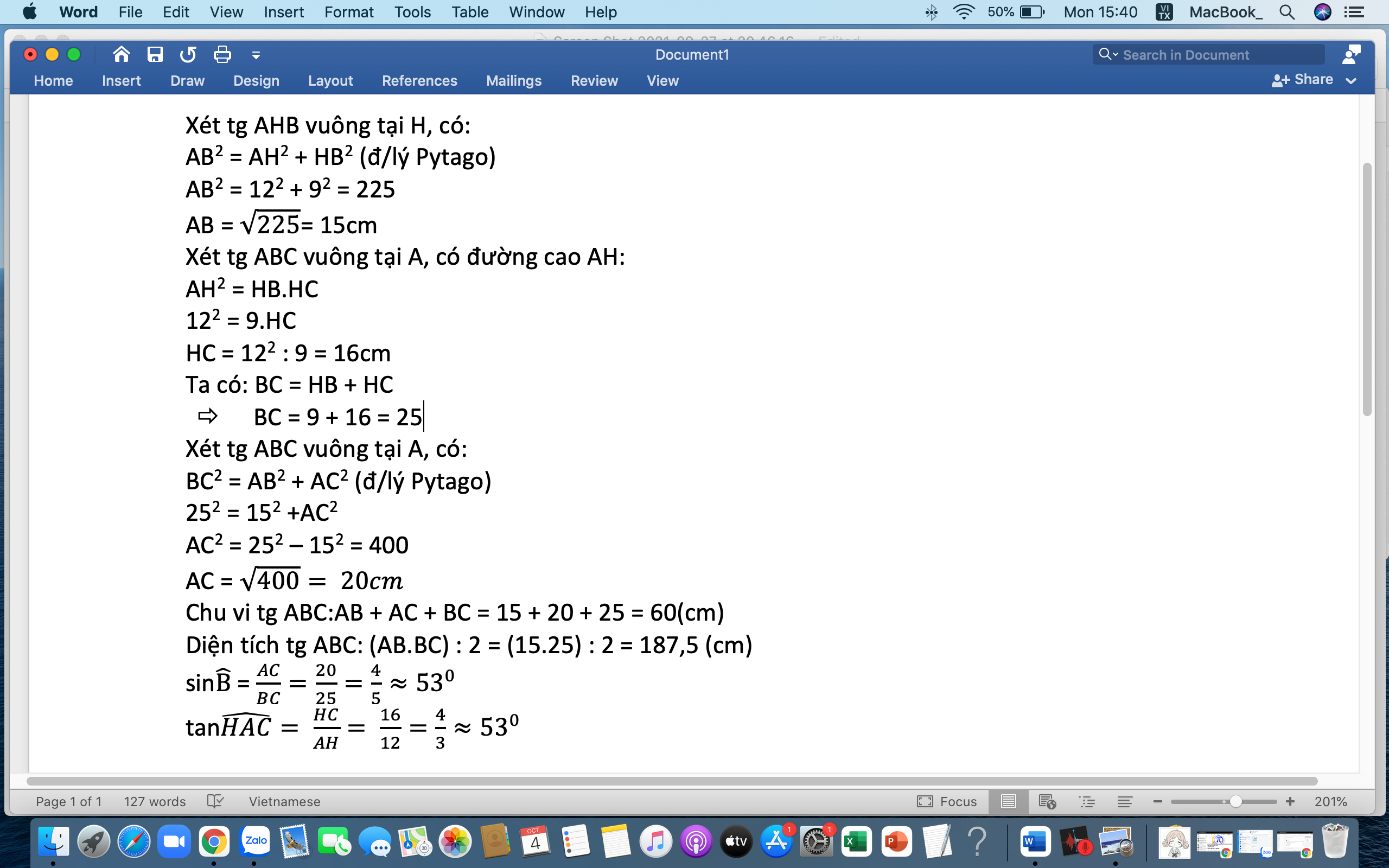
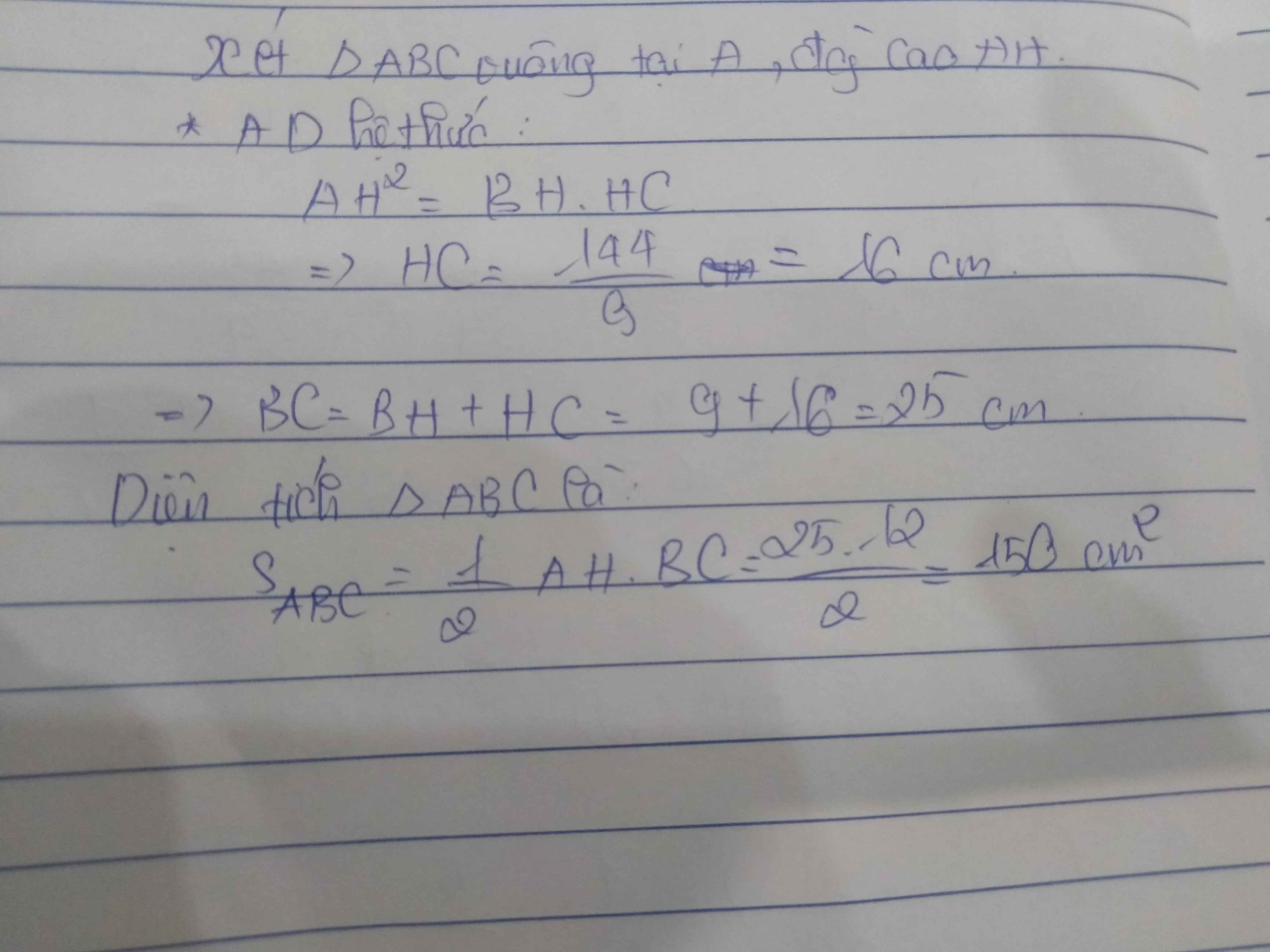Cho tam giác ABC vuông tại A, chu vi 60cm, đường cao AH = 12cm. Tính diện tích tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 10 2021
Áp dụng HTL:
\(AH^2=BH.HC\)
\(\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{12^2}{9}=16\left(cm\right)\)
\(\Rightarrow BC=BH+HC=16+9=25\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.12.25=150\left(cm^2\right)\)
NT
Cho Tam giác ABC vuông tại A , đường cao AH . Tính diện tích Tam giác ABC , biết AH = 12cm , BH= 9cm
3
MN
13 tháng 7 2021
Áp dụng HTL trong tam giác vuông ABC :
\(AH^2=BH\cdot CH\)
\(\Rightarrow CH=\dfrac{12^2}{9}=16\left(cm\right)\)
\(BC=BH+CH=9+16=25\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot12\cdot25=150\left(cm^2\right)\)
NL
3
7 tháng 8 2021
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=HB.HC\Rightarrow HB=\dfrac{AH^2}{HC}=\dfrac{144}{16}=9\)cm
-> BC = HB + HC = 9 + 16 = 25 cm
Diện tích tam giác ABC là : \(S_{ABC}=\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.12.25=150\)cm2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
Áp dụng hệ thức lượng:
\(AB^2=BH.CH\Rightarrow BH=\dfrac{AH^2}{CH}=9\left(cm\right)\)
\(\Rightarrow BC=BH+CH=25\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=150\left(cm^2\right)\)
13 tháng 6 2021
a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)
\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)
* Áp dụng hệ thức :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)
\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)
\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm
\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm
\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)
Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm2
13 tháng 6 2021
b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Lại có : \(BC=BD+DC=15+20=35\)cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)
\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm
\(\Rightarrow AB=\frac{3}{4}.28=21\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm
\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm
Áp dụng định lí Pytago cho tam giác AHD vuông tại H
\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm
22 tháng 8 2020
Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~
