Bt: Tìm GTLN của bt : \(B=-x^2+\sqrt{5}x-2\). GTLN đó đạt đc khi nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LD
2
HF
28 tháng 7 2020
+) \(B=6\sqrt{x-2}+6\sqrt{5-x}\Leftrightarrow B^2=\left(6\sqrt{x-2}+6\sqrt{5-x}\right)^2\)
\(=36\left(x-2\right)+36\left(5-x\right)+72\sqrt{\left(x-2\right)\left(5-x\right)}\ge108\Rightarrow B\ge6\sqrt{3}\)
+) \(A=B+2\sqrt{5-x}\ge6\sqrt{3}\)
Vậy \(A_{min}=6\sqrt{3}\)khi x=5
HF
28 tháng 7 2020
+) Đặt \(a=\sqrt{x-2};b=\sqrt{5-x}\)
+) Ta có: \(a^2+b^2=3\)
+) \(\left(a^2+b^2\right)\left(6^2+8^2\right)\ge\left(6a+8b\right)^2\Leftrightarrow\left(6a+8b\right)^2\le300\Rightarrow6a+8b\le10\sqrt{3}\)
Dấu = xảy ra khi \(\frac{a}{6}=\frac{b}{8}\Leftrightarrow\frac{\sqrt{x-2}}{6}=\frac{\sqrt{5-x}}{8}\Leftrightarrow\frac{x-2}{36}=\frac{5-x}{64}\Leftrightarrow64x-128=180-36x\Leftrightarrow308=100x\)
\(\Leftrightarrow x=3.08\)
Vậy \(A_{max}=10\sqrt{3}\)khi x=3.08
HH
21 tháng 10 2015
\(x^2\ge0\)
\(16-x^2\le16\)
\(\sqrt{16-x^2}\le\sqrt{16}\left(-4\le x\le4\right)\)
\(A\le4\)
Vậy GTLN của A là 4 khi x=0
MN
1
2 tháng 11 2016
x2 + y2 = \(\sqrt{9-4\sqrt{5}}+\sqrt{14-6\sqrt{5}}\) = \(\sqrt{5}-2+3-\sqrt{5}=1\)
Ta có
P = xy \(\le\frac{x^2+y^2}{2}=\frac{1}{2}\)
AH
Akai Haruma
Giáo viên
12 tháng 1 2022
Lời giải:
ĐKXĐ: $x\geq 0$
Áp dụng BĐT Cô-si: $x+1\geq 2\sqrt{x}$
$\Rightarrow \frac{3\sqrt{x}}{x+1}\leq \frac{3\sqrt{x}}{2\sqrt{x}}=\frac{3}{2}$
Vậy gtln của bt là $\frac{3}{2}$ khi $x=1$
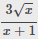
đạt gtnn là 17/4 khi x=căn bậc hai của 5 rồi chia cho 2 (2 không nằm trong dấu căn)