K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VD
1
10 tháng 11 2020
\(y=\frac{x}{\left(x+2011\right)^2}\)
Với x ≤ 0 => y ≤ 0
Với x > 0
Áp dụng bất đẳng thức Cauchy ta có :
\(x+2011\ge2\sqrt{2011x}\)
⇔ \(\left(x+2011\right)^2\ge8044x\)
⇔ \(\frac{1}{\left(x+2011\right)^2}\le\frac{1}{8044x}\)
⇔ \(\frac{x}{\left(x+2011\right)^2}\le\frac{1}{8044}\)
Đẳng thức xảy ra khi x = 2011
=> yMax = 1/8044 <=> x = 2011
TL
1
21 tháng 5 2016
TÌm x > 0 để B = \(\frac{x}{\left(x+2011\right)^2}\)đạt GTLN. Tìm GTLN.
8 tháng 11 2021
\(=-\left(16x^2-16x-2\right)\)
\(=-\left(16x^2-2\cdot4x\cdot2+4-6\right)\)
\(=-\left(4x-2\right)^2+6\le6\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
NK
1
13 tháng 11 2021
\(D=\dfrac{2\left(\sqrt{x}-1\right)+9}{\sqrt{x}-1}=2+\dfrac{9}{\sqrt{x}-1}\)
Vì \(\dfrac{9}{\sqrt{x}-1}\le\dfrac{9}{0-1}=-9\Leftrightarrow D\le2-9=-7\)
Vậy \(D_{max}=-7\Leftrightarrow x=0\)
NN
0
21 tháng 5 2019
Ta có P=\(\frac{20-x-5\sqrt{x}+4\sqrt{x}}{\sqrt{x}+5}\)
P=\(\frac{\sqrt{x}\left(4-\sqrt{x}\right)+5\left(4-\sqrt{x}\right)}{\sqrt{x}+5}\)
P=\(\frac{\left(\sqrt{x}+5\right).\left(4-\sqrt{x}\right)}{\sqrt{x}+5}\)
P=\(4-\sqrt{x}\)
b) Ta có P=\(4-\sqrt{x}\)\(\le\)4 với mọi x\(\ge0\)
=> P đạt GTLN là 4 khi \(\sqrt{x}=0\)
=> x=0
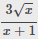
Lời giải:
ĐKXĐ: $x\geq 0$
Áp dụng BĐT Cô-si: $x+1\geq 2\sqrt{x}$
$\Rightarrow \frac{3\sqrt{x}}{x+1}\leq \frac{3\sqrt{x}}{2\sqrt{x}}=\frac{3}{2}$
Vậy gtln của bt là $\frac{3}{2}$ khi $x=1$