Cho f(x) = 1+ x3+x5+x7+...+x101
Tính f(1) và f(-1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
1
HK
2
PT
1 tháng 7 2021
Thay x = 1 vào f(x) ta được
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
1 tháng 7 2021
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
CM
18 tháng 10 2017
Thay x = 1 vào f(x) ta được
f ( 1 ) = 1 + 1 3 + 1 5 + 1 7 + … + 1 101 = 1 + 1 + 1 + … + 1 ⏟ 51501 = 51.1 = 51
Thay x = -1 vào f(x) ta được
f ( − 1 ) = 1 + ( − 1 ) 3 + ( − 1 ) 5 + ( − 1 ) 7 + … + ( − 1 ) 101 = 1 + ( − 1 ) + ( − 1 ) + … + ( − 1 ) ⏟ 50 : 0 ( − 1 ) = 1 + 50. ( − 1 ) = 1 − 50 = − 49 Vây f ( 1 ) = 51 ; f ( − 1 ) = − 49
Chọn đáp án B
CM
1 tháng 1 2017
f(x) = x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7
= (x5 + x5) + (3x2 + 2x2 – 4x2) + (-5x3 + x3) + (-x7 + x7)
= 2x5 + x2 – 4x3.
= 2x5 - 4x3 + x2
Đa thức có bậc là 5
g(x) = x4 + 4x3 – 5x8 – x7 + x3 + x2 – 2x7 + x4 – 4x2 – x8
= (x4 + x4) + (4x3 + x3) – (5x8 + x8) – (x7 + 2x7) + (x2 – 4x2)
= 2x4 + 5x3 – 6x8 – 3x7 – 3x2
= -6x8 - 3x7 + 2x4 + 5x3 - 3x2.
Đa thức có bậc là 8.
ND
1
PT
1
CM
4 tháng 7 2018
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7
= x7 - (3x2+ x2) – x5+ x4 + 2x – 7
= x7 – 4x2 – x5+ x4 + 2x – 7
= x7 – x5 + x4 – 4x2 + 2x - 7
g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1
= x – ( 2x2 + 4x2) + x4 – x5 –x7 – 1
= x – 6x2 + x4 – x5 – x7 – 1
= -x7 – x5 + x4 – 6x2 + x – 1
* f(x) – g(x)
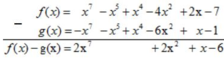
Vậy f(x) – g(x) = 2x7 + 2x2 + x - 6
f(1) = 1^1 + 1^3 + 1^5 + 1^7 +... +1^101
= 1+1+1+...+1
Bieu thuc tren co so so hang la : (101-1):2+1=51 so
f(1)=1.51=51
f(-1) = 1 + (-1)^3+(-1)^5+(-1)^7+...+(-1)^101
= 1 + (-1)+(-1)+(-1)+...+(-1)
Trong biểu thuc tren tu (-1)^3 den (-1)^101 co so so hang la : (101-3):2+1=47
f(-1)=1+(-1).47=1+(-1)=0