Cho góc xAy < 90°. Trên tia Ax lấy 2 điểm B và C (AB<AC). Trên tia Ay lấy 2 điểm D và E sao cho BD//CE. Giả sử AB=6cm, BC=9cm, DE=3cm. Tính AC và AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOAB và ΔOAC có
OA chung
\(\widehat{BAO}=\widehat{CAO}\)
OB=OC
Do đó: ΔOAB=ΔOAC
b: Xét ΔOBM và ΔOCN có
OB=OC
\(\widehat{OBM}=\widehat{OCN}\)
BM=CN
Do đó: ΔOBM=ΔOCN

a) Xét 2 tam giác ABD và ADC có :
AB = AC (gt)
Góc BAD = Góc DAC
AD chung
=> : BAD = ADC (c.g.c). Vậy Góc ABC = Góc ACB.
b) Từ chứng minh trên ta có : Góc ADC = Góc ADB. Mà 2 góc đó lại kề bù với nhau : => Góc ADC = Góc ADB = 90 độ

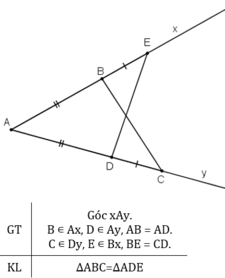
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.
Xét ΔABC và Δ ADE có:
AC = AE (cmt)
Góc A chung
AB = AD (gt)
⇒ ΔABC = ΔADE (c.g.c)

a/ Ta có: AD=2cm, AB=4cm, AE=12cm, AC=6cm
\(=>\left\{{}\begin{matrix}\dfrac{AD}{AB}=\dfrac{2}{4}=\dfrac{1}{2}\\\dfrac{AE}{AC}=\dfrac{12}{6}=2\end{matrix}\right.\)
\(=>\dfrac{AE}{AC}>\dfrac{AD}{AB}\)

Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC

Xét ΔABC và ΔADE có
AB=AD
\(\widehat{BAC}\) chung
AC=AE
Do đó: ΔABC=ΔADE
Suy ra: \(\widehat{MCD}=\widehat{MEB}\)
Xét ΔCBE và ΔEDC có
CB=ED
CE chung
BE=DC
Do đó: ΔCBE=ΔEDC
Suy ra: \(\widehat{MBE}=\widehat{MDC}\)
Xét ΔMBE và ΔMDC có
\(\widehat{MBE}=\widehat{MDC}\)
BE=DC
\(\widehat{MEB}=\widehat{MCD}\)
Do đó: ΔMBE=ΔMDC
Suy ra: ME=MC
Xét ΔAME và ΔAMC có
AM chung
ME=MC
AE=AC
Do đó: ΔAME=ΔAMC
Suy ra: \(\widehat{EAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc xAy
cjhiuj