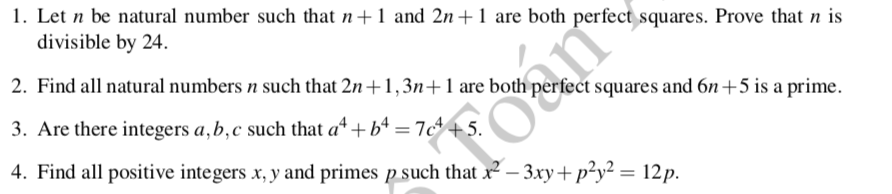tìm tất cả các sô tự nhiên n sao cho : 7^n+147 là số chình phương.Ai giúp mình bài này với.tks nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
24 tháng 6 2020
Vì \(7^n+147\) là số chính phương
=> Đặt: \(7^n+147\) với a là số nguyên khi đó ta có:
\(7^n+147=a^2\)không mất tính tổng quát g/s a nguyên dương
mà: n là số tự nhiên nên \(7^n⋮7\); \(147=7^2.3⋮7\)=> \(a^2⋮7\)=> \(a⋮7\)=> \(a^2⋮7^2\)
=> \(7^n⋮7^2\)=> n \(\ge\)2
+) Với n = 2k khi đó: \(k\ge1\)
Ta có: \(7^{2k}+147=a^2\)
<=> \(\left(a-7^k\right)\left(a+7^k\right)=147\)
Vì: \(\hept{\begin{cases}0< a-7^k< a+7^k\\a-7^k;a+7^k⋮7\end{cases}}\)
Do đó: \(\hept{\begin{cases}a+7^k=21\\a-7^k=7\end{cases}}\Leftrightarrow7^k=7\Leftrightarrow k=1\)=> n = 2
Thử lại thỏa mãn
+) Với n = 2k + 1 ta có:
\(7^{2k+1}:4\) dư -1
\(147\): 4 dư 3
=> \(7^{2k+1}+147\) chia 4 dư 2
mà số chính phương chia 4 bằng 0 hoặc 1
=> Loại
Vậy: n = 2
CH
Cô Hoàng Huyền
Admin
VIP
8 tháng 1 2018
Câu hỏi của Nguyễn Lịch Tiểu - Toán lớp 6 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2022
1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau
6 tháng 12 2016
bai2
UCLN (n,n+2)=d
=>(n+2)-n chia hết cho d
2 chia het cho d
vay d thuoc uoc cua 2={1,2}
nếu n chia hết cho 2 uoc chung lon nhta (n,n+2) la 2
neu n ko chia het cho 2=> (n,n+2) nguyen to cung nhau
BCNN =n.(n+2) neu n le
BCNN=n.(n+2)/2
30 tháng 10 2021
ta có:5n + 14 chia hết cho n + 2
=>5(n + 2)+4 chia hết cho n + 2
=>4 chia hết cho n + 2
=>n+2 thuộc ước của 4={1;-1;2;-2;4;-4}
=>n ={-1;-3;0;-4;2;-6}
30 tháng 10 2021
BL
Ta có 5n+16=5n+10+6
Vì 5n+16\(⋮\)n+2
=>5n+10+6\(⋮\)n+2
=>6\(⋮\)n+2 Vì 5n+10 \(⋮\) n+2
=>\(n+2\inƯ\left(6\right)\)
mà Ư(6)={-1;1;-2;2;-3;3;-6;6}
Ta có bảng
| n+2 | -1 | 1 | -2 | 2 | -3 | 3 | -6 | 6 |
| n | -3 | -1 | -4 | 0 | -5 | 1 | -8 | 4 |
vậy .........
NT
0
NM
Nguyễn Minh Quang
Giáo viên
3 tháng 9 2021
xét mọi số chính phương đều có thể viết dưới dạng :
\(\left(a\cdot n+b\right)^2\) với mọi số \(a,b\) là các số tự nhiên và b nhở hơn n
mà ta có :
\(\left(a\cdot n+b\right)^2=a^2\cdot n^2+2ab\cdot n+b^2\equiv b^2mod\left(n\right)\)
vậy \(b^2< n\forall b< n\)điều này chỉ đúng khi n=2
vậy n=2
