choa hình thang ABCD(AB//CD)và AB<CD.Đường chéo BD vg góc vs canhjbeen BC. Vẽ đường cao BH
a,c/m hai tam giác BDC và HBC đồng dạng
b,cho BC=15cm,DC=25cm; Tính HC và HD
c, Tính diện tích hình thang ABCD
ai làm hộ mình vs ạ mình đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HB
1
NR
2 tháng 9 2016
Vì ABCD là hình thang cân nên AB=AD=BC
Tam giác ACD cân tạ C, ta có: góc DAC=góc ADC
Tam giác ABC cân tại B, ta có: góc BAC= góc ACB
Mặt khác: góc ACB= góc ACD (vì góc ACD= góc BAC (so le trong))= gócBCD/2 = góc ADC/2
Ta có: góc DAB + góc ADC= góc DAC+góc BAC+góc ADC= 2.góc ADC+góc ACD/2=180 độ (vì AB//CD)→ góc ADC=72 độ
BN
3
2 tháng 9 2016
Uhm! Câu này khó đấy ! Mình cứ làm không biết có đúng không nhé. Hi
Đầu tiên bạn vẽ hình ra.
*Vì đây là hình thang cân nên ta có những điều sau:
-AB//CD
-2 đường chéo bằng nhau : AC=BD=CD (theo giả thiết)
-2 cạnh bên bằng nhau: AD=BC=AB (theo giả thiết)
-tổng 2 góc đối nhau = 180 độ
-góc A=B ; góc C=D
Đặt các góc:ADB=D1 ; BDC=D2 ;ACB=C1 ; ACD=C2 ; DBC=B1 ; ABD=B2 ; DAC=A1 ; CAB = A2
*AB=AD suy ra tam giác ADB cân tại A nên góc D1=B2. Mặt khác vì AB//CD nên góc D2 = B2 (sole trong)
=>ADB=ABD=BDC => D1=D2
*AB=BC suy ra tam giác ABC cân tại B nên góc BAC=BCA. tương tự gocA2=C2 (sole trong)
=>A2=C1=C2 =>C1=C2
* Vì gócC=D nên suy ra C1=C2=D1=D2
* Có C2=D1 và lại có D1=B2 (đã chứng minh ở trên) nên C2=B2 (1)
* Xét tam giác BDC có BD=CD (theo giả thiết) nên BDC cân suy ra B1 = C = C1+C2 (2)
* Từ (1) và (2) suy ra B=B1+B2 = C1 + C2 + C2 = 3C2 = 3D2 (vì C2=D2 - CM trên thêm nữa góc D= D1 + D2 = 2D2 )
* Mà góc B+D = 180* nên suy ra 3.D2 + 2.D2 = 180* <=> 5.D2=180* <=> D2=36*
Suy ra D = C = 36 x 2 = 72*
A = B = 36 x 3 = 108*
26 tháng 7 2017
*Vì đây là hình thang cân nên ta có những điều sau:
-AB//CD
-2 đường chéo bằng nhau : AC=BD=CD (theo giả thiết)
-2 cạnh bên bằng nhau: AD=BC=AB (theo giả thiết)
-tổng 2 góc đối nhau = 180 độ
-góc A=B ; góc C=D
Đặt các góc:ADB=D1 ; BDC=D2 ;ACB=C1 ; ACD=C2 ; DBC=B1 ; ABD=B2 ; DAC=A1 ; CAB = A2
*AB=AD suy ra tam giác ADB cân tại A nên góc D1=B2. Mặt khác vì AB//CD nên góc D2 = B2 (sole trong)
=>ADB=ABD=BDC => D1=D2
*AB=BC suy ra tam giác ABC cân tại B nên góc BAC=BCA. tương tự gocA2=C2 (sole trong)
=>A2=C1=C2 =>C1=C2
* Vì gócC=D nên suy ra C1=C2=D1=D2
* Có C2=D1 và lại có D1=B2 (đã chứng minh ở trên) nên C2=B2 (1)
* Xét tam giác BDC có BD=CD (theo giả thiết) nên BDC cân suy ra B1 = C = C1+C2 (2)
* Từ (1) và (2) suy ra B=B1+B2 = C1 + C2 + C2 = 3C2 = 3D2 (vì C2=D2 - CM trên thêm nữa góc D= D1 + D2 = 2D2 )
* Mà góc B+D = 180* nên suy ra 3.D2 + 2.D2 = 180* <=> 5.D2=180* <=> D2=36*
Suy ra D = C = 36 x 2 = 72*
A = B = 36 x 3 = 108*
CM
14 tháng 4 2018
Kẻ BH ^ CD tại H Þ BH = B C 2 = 4cm.
Tính được SABCD = 22cm2
4 tháng 8 2021
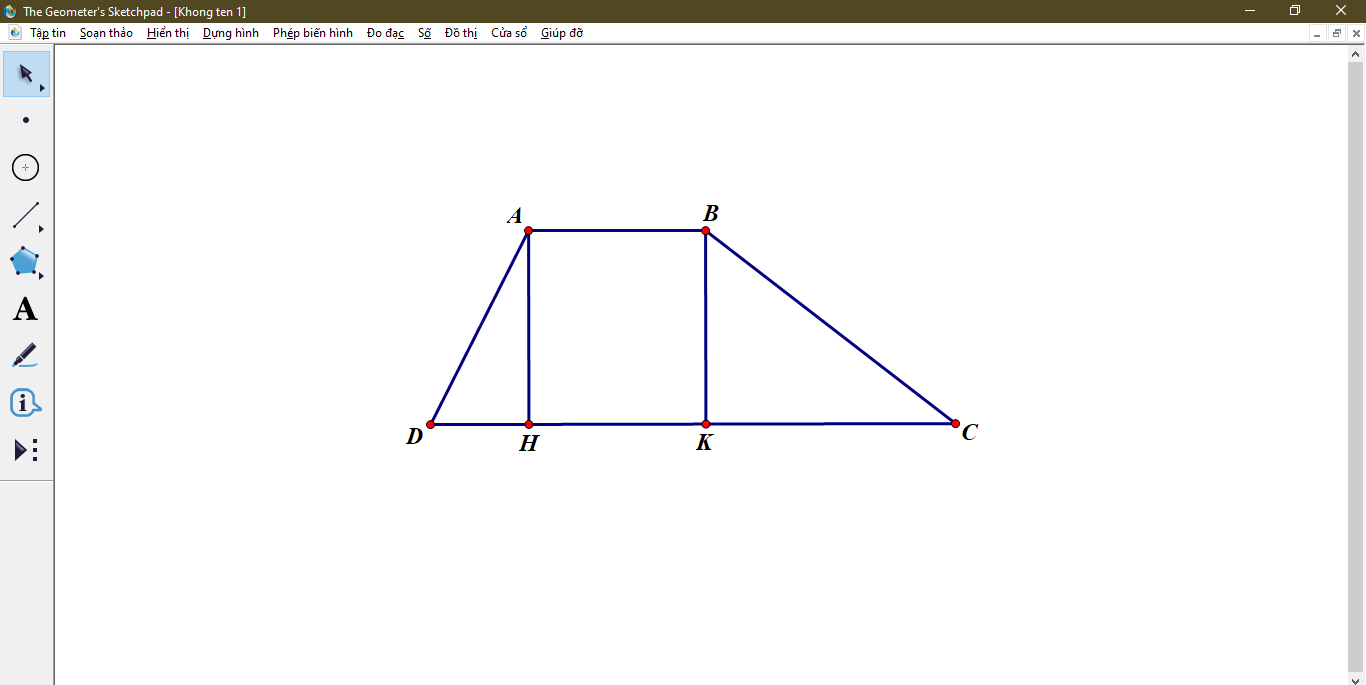
Kẻ đường cao AH và đường cao BK . ⇒AB=HK=1cm
Nên ta có : DH+CK=4 (1)
Theo tỉ số lượng giác cho tam giác ADH và BCK ta lại có :
\(\left\{{}\begin{matrix}AH=tan60\cdot DH\\BK=tan30\cdot CK\end{matrix}\right.\)\(\Rightarrow tan60\cdot DH=tan30\cdot CK\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình :
\(\left\{{}\begin{matrix}DK+CK=4\\\sqrt{3}DH-\dfrac{\sqrt{3}}{3}CK=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DH=1\\CK=3\end{matrix}\right.\)
\(\Rightarrow AH=tan60\cdot DH=\sqrt{3}\cdot1=\sqrt{3}\left(cm\right)\)
\(\Rightarrow S_{ABCD}=12\cdot AH\cdot\left(AB+CD\right)=12\cdot\sqrt{3}\cdot\left(1+5\right)=3\sqrt{3}\left(cm^2\right)\)
Tick hộ nha bạn 😘
a, Ta có SBDC = DB.BC = BH.DC ⇒ DB/BH=DC/BC
Ta có ∠BHD = ∠DBC (=90 độ)
⇒ △BDC ∼ △HBC (T/c đồng dạng thứ 3)
b, Áp dụng đ/lí Pitago vào △ vuông DBC, ta có:
DC2=BD2 + BC2 ⇒ BD2=400 ⇒ BD=20 cm
Từ câu a, DB.BC = BH.DC ⇒ BH = 300/25 = 12 cm
Áp dụng đ/lí Pitago vào △ vuông DBH, ta có:
DB2 = DH2 + BH2 ⇒ DH = 16 cm
Ta có HC = DC - DH = 25 - 16 = 9 cm