Một con lắc lò xo có khối lượng m = 200 g đồng thời thực hiện hai dao động điều hoà cùng phương có phương trình: x1 = 6cos(5πt - π/2) cm và x2 = 6cos5πt cm. Lấy π2 = 10. Cơ năng dao động của vật là
A. 180 mJ. B. 90 mJ.
C. 900 J. D. 180 J.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+ Hai dao động vuông pha: A = A 1 2 + A 2 2 = 6 2 ( c m )
+ x = 2 2 cm => x = A 3 => Wt = 1 2 mω2x2 = 1 18 mω2A2
+ Wđ = W – Wt = 1 2 mω2A2 - 1 18 mω2A2 = 4 9 mω2A2
⇒ W đ W t = 8

Chọn C
+ Hai dao động vuông pha: A = A 1 2 + A 2 2 = 8 2 ( c m )
+ Wđ = W – Wt = 1 2 mω2A2 - 1 2 mω2x2 = 1 2 mω2A2 - 1 2 mω2 ( A 2 ) 2
= 3 8 mω2A2 = 3 8 . 0,5.(2π)2. (8 2 .10-2) 2 = 0,096 J = 96mJ.

Hướng dẫn: Chọn đáp án B
![]()
![]()
Dùng máy tính Casio fx 570 – ES, bấm như sau:
![]() (Để chọn đơn vị góc là radian)
(Để chọn đơn vị góc là radian)
![]() (Để chọn chế độ tính toán với số phức)
(Để chọn chế độ tính toán với số phức)
![]()
(Màn hình máy tính sẽ hiện thị 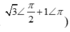

pha ban đầu φ = 2 π 3 nên ta sẽ chọn B.
Chú ý: Để thực hiện phép tính về số phức, bấm: MODE 2 màn hình xuất hiện CMPLX.
Muốn biểu diện số phức dạng A ∠ φ , bấm SHIFT 2 3 =
Muốn biểu diện số phức dạng: a + bi , bấm SHIFT 2 4 =
Để nhập ký tự ∠ bấm: SHIFT (-)
Khi nhập các số liệu thì phải thống nhất được đơn vị đo góc là độ hay rađian
Nếu chọn đơn vị đo là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị chữ D
Nếu chọn đơn vị đo là Rad (R), bấm: SHIFT MODE 4 màn hình hiển thị chữ R.

Đáp án D
Phương pháp: Áp dụng công thức tính biên độ tổng hợp của hai dao động cùng phương, cùng tần số và công thức tính năng lượng của con lắc lò dao động điều hoà
Cách giải:
Dao động của vật là tổng hợp hai dao động thành phần có biên độ A = 10cm = 0,1m, tần số góc ω = 10 rad/s
Vật có m = 500g = 0,5kg.
Năng lượng dao động của vật là:
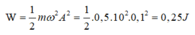
\(\Delta\varphi=\varphi_2-\varphi_1=\dfrac{\pi}{2}\)
\(A=\sqrt{A_1^2+A_2^2}=6\sqrt{2}\left(cm\right)\)
Phương trình dao động tổng hợp: \(x=6\sqrt{2}cos\left(5\pi t+\dfrac{\pi}{2}\right)cm\)
Cơ năng dao động của vật là:
\(W=\dfrac{1}{2}m\omega^2A^2=\dfrac{1}{2}.0,2.\left(5\sqrt{10}\right)^2.\left(6\sqrt{2}.10^{-2}\right)^2=0,18\left(J\right)=180\left(mJ\right)\)
Chọn A.