Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Hai dao động vuông pha: A = A 1 2 + A 2 2 = 8 2 ( c m )
+ Wđ = W – Wt = 1 2 mω2A2 - 1 2 mω2x2 = 1 2 mω2A2 - 1 2 mω2 ( A 2 ) 2
= 3 8 mω2A2 = 3 8 . 0,5.(2π)2. (8 2 .10-2) 2 = 0,096 J = 96mJ.

Đáp án A
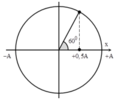
Tại thời điểm t = 0, vật ở vị trí biên dương. Vị trí động năng bằng 3 lần thế năng ứng với x = ±0,5A
→ Biểu diễn dao động của vật tương ứng trên đường tròn
+ Từ hình vẽ, ta có T 6 = 1 30 → T = 0,2 s
→ Độ cứng của lò xo T = 2 π m k → 0 , 2 = 2 π 50.10 − 3 k → k = 50 N/m

\(\Delta\varphi=\varphi_2-\varphi_1=\dfrac{\pi}{2}\)
\(A=\sqrt{A_1^2+A_2^2}=6\sqrt{2}\left(cm\right)\)
Phương trình dao động tổng hợp: \(x=6\sqrt{2}cos\left(5\pi t+\dfrac{\pi}{2}\right)cm\)
Cơ năng dao động của vật là:
\(W=\dfrac{1}{2}m\omega^2A^2=\dfrac{1}{2}.0,2.\left(5\sqrt{10}\right)^2.\left(6\sqrt{2}.10^{-2}\right)^2=0,18\left(J\right)=180\left(mJ\right)\)
Chọn A.

Chọn B
+ Hai dao động vuông pha: A = A 1 2 + A 2 2 = 6 2 ( c m )
+ x = 2 2 cm => x = A 3 => Wt = 1 2 mω2x2 = 1 18 mω2A2
+ Wđ = W – Wt = 1 2 mω2A2 - 1 18 mω2A2 = 4 9 mω2A2
⇒ W đ W t = 8

Đáp án B
Phương pháp: Chu ki dao đông̣ điều hoa cua con lắc lo xo T = 2 π m k
Cách giải:
Theo bài ra ta có
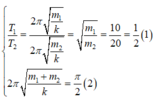
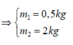

1. Chu kì 2 vật là:
\(T_1=2\pi\sqrt{\dfrac{m_1}{k_1}}\)
\(T_2=2\pi\sqrt{\dfrac{m_2}{k_2}}\)
Có \(T_1=T_2\)
\(\Rightarrow \dfrac{m_1}{k_1}=\dfrac{m_2}{k_2}\)
\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{m_2}{m_1}=3\)
Mà với 1 lò xo thì \(k.l=const\)
\(\Rightarrow k_1.l_1=k_2.l_2\)
\(\Rightarrow k_1.CA=k_2.CB\)
\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{CA}{CB}=3\)
\(\Rightarrow \dfrac{CA}{CA+CB}=\dfrac{3}{3+1}\)
\(\Rightarrow \dfrac{CA}{AB}=\dfrac{3}{4}\)
Tần số dao động:
\(f_1=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_1}}\)
\(f_2=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_2}}\)
Ta có: \(\dfrac{f_1}{f_2}=\sqrt{\dfrac{m_2}{m_1}}=\dfrac{10}{5}=2\)
\(\Rightarrow \dfrac{m_1}{m_2}=4\)
Nếu treo cả 2 quả cầu vào lò xo thì chu kì là: \(T=2\pi\sqrt{\dfrac{m_1+m_2}{k}}=2\pi\sqrt{\dfrac{m_1+\dfrac{m_1}{4}}{96}}=\dfrac{\pi}{2}\)
\(\Rightarrow m_1 = 4,8kg\)

\(\Delta t=\frac{T}{4}=\frac{2\pi\sqrt{\frac{k}{m}}}{4}=\frac{\pi}{2}\sqrt{\frac{m}{k}\Rightarrow\Delta t^2=\frac{\pi^{2.}.m}{4k}\Rightarrow k=\frac{m^{2.}.n}{4\Delta t^2}=\frac{10.0,05}{4.0,05^2}=\frac{10}{4.0,005}}=\frac{50N}{m}\)

Giải thích: Đáp án D
Phương pháp:
Sử dụng lí thuyết về khoảng cách của hai vật dao động điều hoà
Khảo sát hàm số bậc hai
Cách giải:
Phương trình dao động của vật A là ![]()
Phương trình dao động của vật B là ![]()
Mặt khác: 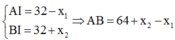
Có:
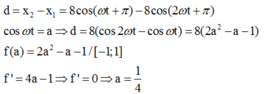
Xét bảng biến thiên sau:
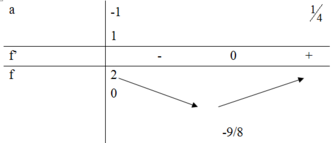
Từ bảng biến thiên ta có:
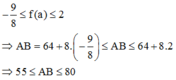
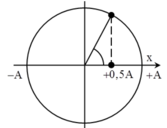

Đáp án D
Phương pháp: Áp dụng công thức tính biên độ tổng hợp của hai dao động cùng phương, cùng tần số và công thức tính năng lượng của con lắc lò dao động điều hoà
Cách giải:
Dao động của vật là tổng hợp hai dao động thành phần có biên độ A = 10cm = 0,1m, tần số góc ω = 10 rad/s
Vật có m = 500g = 0,5kg.
Năng lượng dao động của vật là: