Cho tam giác ABC cân tại A có AB = 14 cm. Đường trung trực của AB cắt AC tại E. Chu vi tam giác BEC = 24 cm. Tính BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
19 tháng 8 2016
Tam giác ABC cân tại A => AC = AB = 14 cm
Vì E thuộc đường trung trực của AB => EA = EB
=> EA + EC = EB + EC = AC = 14 cm
chu vi tam giác BEC = 24 cm => EB + EC + BC = 24 cm
=> BC = 24 - ( EB + EC )
=> 24 - 14 = 10 cm
Vậy đoạn thẳng BC dài 10 cm .
19 tháng 8 2016
Bạn vẽ hình của ▲ABC ra, vẽ trung trực AB cắt AC tại E.
Nhận xét ▲ABE có: AE = BE (do E thuộc đường trung trực của AB)
Chu vi ▲BEC là:
P▲BEC = BE + EC + BC
mà AE = BE
---> P▲BEC = AE + EC + BC = AC+ BC
---> BC = P▲BEC - AC = 24 - 14 = 10cm
CM
20 tháng 10 2018
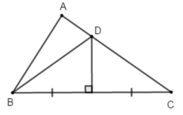
D thuộc đường trung trực của đoạn thẳng BC nên DB = DC (tính chất điểm thuộc đường trung trực của đoạn thẳng)
Chu vi tam giác ABD là:
AB + DB + AD = AB + DC + AD = AB + (CD + AD) = AB + AC = 16 + 25 = 41 cm
Vậy chu vi tam giác ABD là 41 cm.
Chọn đáp án B
21 tháng 5 2019
a) \(\Delta ABC\)cân tại A có \(\widehat{BAC}=40^o\)nên \(\widehat{ABC}=\widehat{ACB}=70^o\)
gọi giao điểm của AB với đường trung trực của nó là O
CM : \(\Delta AOD=\Delta BOD\left(c.g.c\right)\)\(\Rightarrow\)\(\Delta ADB\)cân tại D
\(\Rightarrow\widehat{ABD}=\widehat{BAD}=70^o\); \(AD=BD\)( 1 )
\(\Rightarrow\widehat{A_1}=\widehat{C_1}=180^o-70^o=110^o\)
Xét \(\Delta BEA\)và \(\Delta CDA\)có :
AE = CD ( gt ) ; \(\widehat{A_1}=\widehat{C_1}\)( cmt ) ; AB = AC ( gt )
\(\Rightarrow\Delta BAE=\Delta ACD\left(c.g.c\right)\)\(\Rightarrow BE=AD\)( 2 )
b) Từ ( 1 ) và ( 2 ) suy ra BE = BD nên \(\Delta BED\)cân tại B
Mà \(\widehat{ADC}=180^o-2.70^o=40^o\)
\(\Rightarrow\widehat{BED}=\widehat{EDB}=40^o\)và \(\widehat{EBD}=100^o\)
13 tháng 1 2023
a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE
10cm nếu muốn bài giải thì bảo nha
Cảm ơn bạn! Mình cũng ra 10cm :))