Làm cách nào để phân biệt cạnh -cạnh- cạnh , cạnh -góc - cạnh , góc -cạnh - góc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-trường hợp c-g-c là 2 cạnh kề với 1 góc.
- trường hợp g.c.g là 2 góc kề với 1 cạnh.
- trường hợp ch-gn là cạnh huyền kề với một góc .
chúc bạn học tốt !!!

Trường hợp bằng nhau góc – cạnh – góc:Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kể của tam giác kia thì hai tam giác đó bằng nhau:
Trường hợp bằng nhau cạnh huyền – góc nhọn của tam giác vuông :
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

thì khi nào nó cho 3 cạnh bằng nhau thì suy ra c-c-c
nó cho hai cạnh và 2 góc ở giữa hai cạnh đó bằng nhau thì suy ra c-g-c
g-c-g thì 2 góc và 1 cạnh nằm giữa hai góc đó của hai tam giác bằng nhau
tương tự với các th còn lại nha bạn

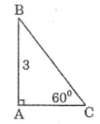
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan60^0=3\sqrt{3}\simeq5,1962\left(cm\right)\)
=>\(BC=\sqrt{AB^2+AC^2}=6\left(cm\right)\)

Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
ti le 3 canh la 3/4/5 (dinh li pytago)
2 canh goc vuong lan luot la
125 : 5 x 4 = 100
125 : 5 x 3 = 75

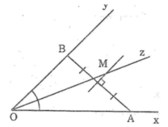
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
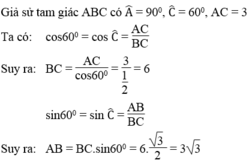

cậu xem lại lý thuyết trong sách giáo khoa nhé