Mọi người giải giúp mình vs ạ. Chiều nay mình phải nộp r 🥺Cảm ơn mn nhiều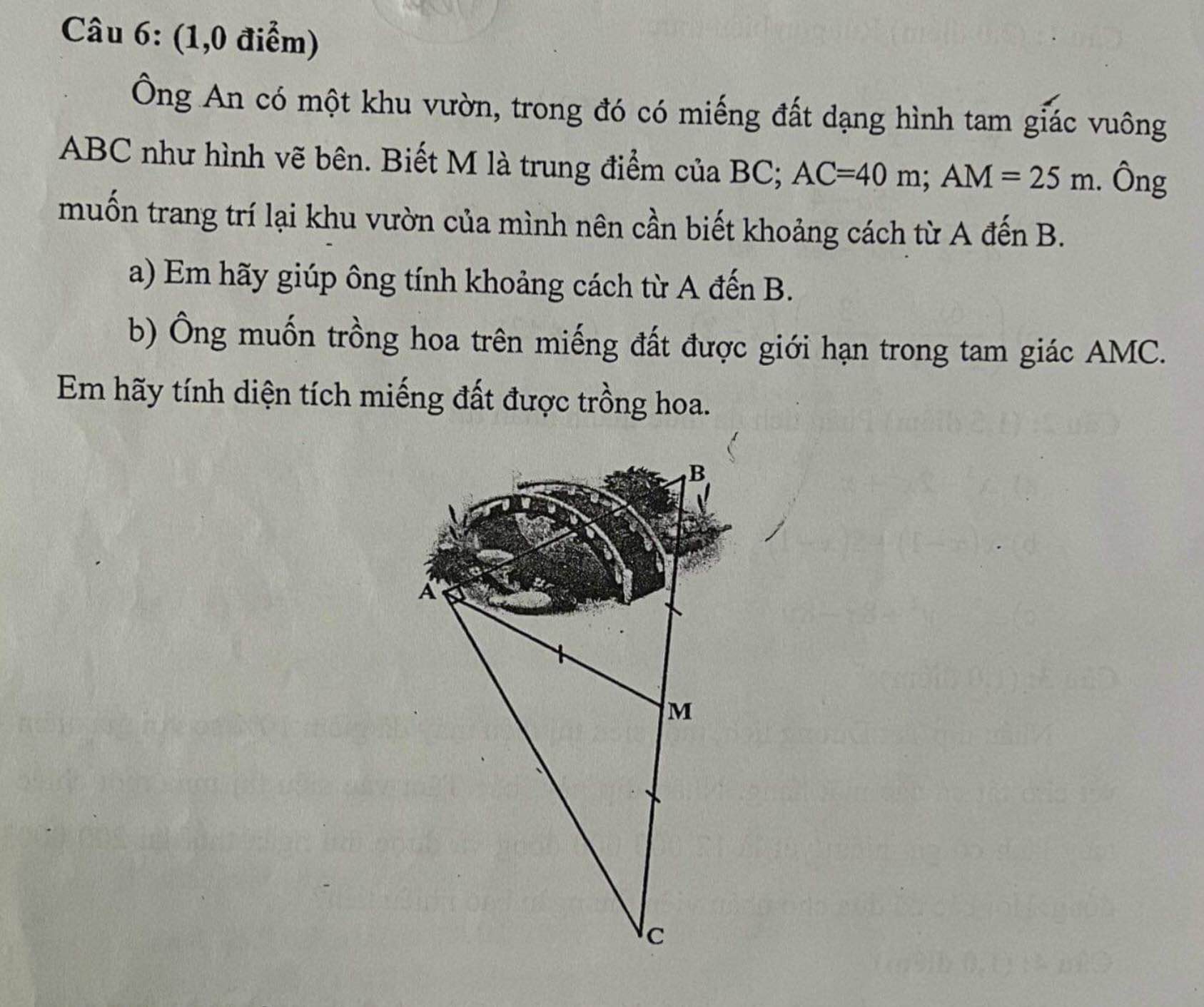
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)



Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)

a: Xét tứ giác ANME có
\(\widehat{ANM}=\widehat{AEM}=\widehat{EAN}=90^0\)
Do đó: ANME là hình chữ nhật

em ơi chưa có bài em nhé, em chưa tải bài lên lám sao mình giúp được



 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều










Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)
Cảm ơn nhiều ạ ;-;