Cho 50 điểm M1,M2,M;...;M50 trên đường thẳng d và điểm O nằm ngoài đường thẳng d . vẽ các tia góc O đi qua 50 điểm đã cho . Hỏi có tất cả bao nhiêu góc đỉnh o mà các cạnh là các tia đã vẽ ở trên?
Giup mình với các bạn !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có M 1 ^ − N 1 ^ = 50 ° (đề bài) (1)
Lại có n // m nên M 1 ^ + N 1 ^ = 180 ° (2) (hai góc trong cùng phía)
Từ (1) và (2) ⇒ 2 M 1 ^ = 230 ° ⇒ M 1 ^ = 115 ° .
Từ (1) có N 1 ^ = 115 ° − 50 ° = 65 ° .
Do n // m nên : N 2 ^ = M 1 ^ = 115 ° (hai góc so le trong).
N 1 ^ = M 2 ^ = 65 ° (hai góc so le trong)

Đáp án B
![]() vtpt của 0x
n
⇀
(1;0;0) vtcp của 0y
m
⇀
(0;1;0)
vtpt của 0x
n
⇀
(1;0;0) vtcp của 0y
m
⇀
(0;1;0)
M 1 là hình chiếu của m lên 0x khi
M M 1 ⇀ . n ⇀ = 0 ⇔ m = 1 suy ra M 1 (1;0;0)
M 2 là hình chiếu của m lên0y khi M M 2 ⇀ . m ⇀ = 0 ⇔ n = 2 suy ra M 2 (0;2;0)
M 1 M 2 ⇀ (-1;2;0) là vtcp của đt M 1 M 2

Tóm tắt:
\(t_1=80^oC\)
\(t_2=10^oC\)
\(t=50^oC\)
\(\Rightarrow\Delta t_1=30^oC\)
\(\Delta t_2=40^oC\)
\(c=4200J/kg.K\)
\(m_1+m_2=700g=0,7kg\)
==============
\(m_1=?kg\)
\(m_2=?kg\)
Khối lượng nước ở 80oC là:
Theo pt cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c.\Delta t_1=m_2.c.\Delta t_2\)
\(\Leftrightarrow m_1.\Delta t_1=m_2.\Delta t_2\)
\(\Leftrightarrow30m_1=40m_2\left(a\right)\)
Mà ta có: \(m_1+m_2=0,7\Rightarrow m_2=0,7-m_1\)
Thay vào (a) ta có:
\(30m_1=40\left(0,7-m_1\right)\)
\(\Leftrightarrow30m_1=28-40m_1\)
\(\Leftrightarrow30m_1+40m_1=28\)
\(\Leftrightarrow70m_1=28\)
\(\Leftrightarrow m_1=\dfrac{28}{70}=0,4\left(kg\right)\)
Khối lượng nước ở 10oC là:
\(m_2=0,7-m_1=0,7-0,4=0,3\left(kg\right)\)

Chọn A
Ta có ![]() và
và 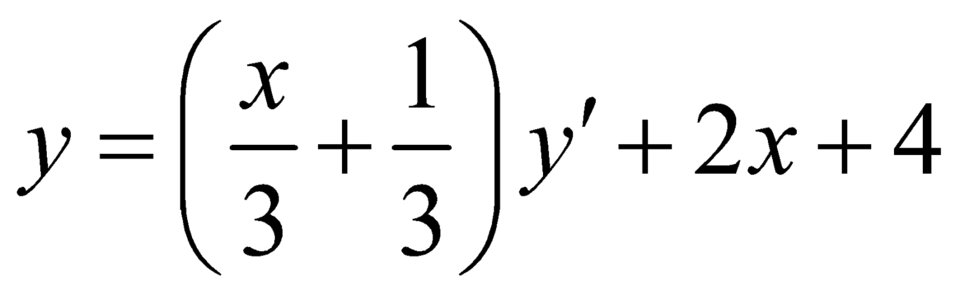 ,
,
Duy ra phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là ![]() ,
, ![]() .
.
Đường tròn ![]() có tâm
có tâm ![]() và bán kính
và bán kính ![]() .
.
Đường thẳng ![]() tiếp xúc với đường tròn
tiếp xúc với đường tròn ![]() khi và chỉ khi
khi và chỉ khi ![]()
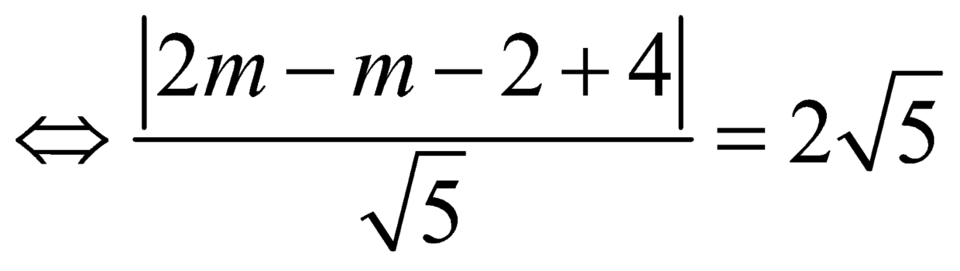
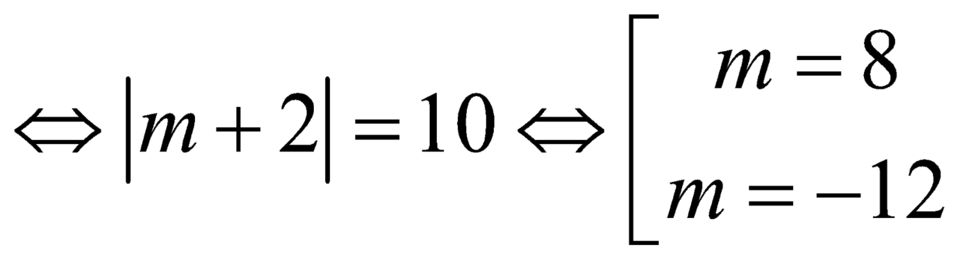 .
.
Vậy ![]() .
.

Đáp án B
Phương pháp:
Giải phương trình y’ = 0 tìm các điểm cực trị B, C của đồ thị hàm số và tính diện tích tam giác OBC.
Cách giải: TXĐ: D = R
Ta có:
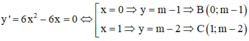
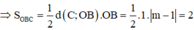

Chọn đáp án B
Ta có y ' = 3 x 2 - 11 . Giả sử M m ; m 3 - 11 m thì tiếp tuyến ∆ của (C) tại điểm M có hệ số góc là k = y ' m = 3 m 2 - 11
Phương trình ∆ : y = 3 m 2 - 11 x - 2 m .
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng ∆ là:
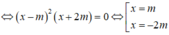
Suy ra hoành độ các điểm Mn lập thành một cấp số nhân (xn) có số hạng đầu x 1 = - 2 và công bội q = -2.
Ta có x n = x 1 . q n - 1 = - 2 n
![]() .
.
Để 11 x n + y n + 2 2019 = 0
⇔ 3 n = 2019 ⇔ n = 673
50.49:2=1225