Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có: y ' = 3 x 2 − 6 x − m 2 + 2
Lấy y y ' thì phần dư ta được PT đường thẳng qua các điểm cực trị là:
y = 2 3 x m 2 + 1 + 2 m 2 + 2 3
Phương trình hoành độ giao điểm là: x 3 − 3 x 2 − m 2 − 2 x + m 2 = 0 ⇔ x 3 − 3 x 2 + 2 x − m 2 x − 1 = 0 ⇔ x − 1 x 2 − 2 x − m 2 = 0 ⇔ x = 1 g x = x 2 − 2 x − m 2 = 0
Đk cắt tại 3 điểm phân biệt ⇔ Δ ' = 1 + m 2 > 0 g ' 1 = − 1 − m 2 ≠ 0
Khi đó C cắt Ox tại 3 điểm A x 1 ; 0 ; B 1 ; 0 ; C x 2 ; 0 , theo Viet ta có: x 1 + x 2 = 2 = 2 x B
Gọi M và N là tọa độ 2 điểm cực trị thì B là trung điểm của MN (Do B là điểm uốn)
Để A M C N là hình chữ nhật thì A C = M N ⇔ x 1 − x 2 = x M − x N 2 + 4 9 m 2 + 1 2 x M − x N 2
Trong đó x M + x N = 2 x M x N = 2 − m 2 3 ⇒ 4 + 4 m 2 = 4 + 4 m 2 − 8 3 4 9 m 2 + 1 2 + 1 ⇔ m 2 + 1 2 = 9 2
m 2 = 3 2 − 1 m 2 = − 3 2 − 1 ⇔ m = ± 3 2 − 1
Do đó T = m 1 4 + m 2 4 = 11 − 6 2

Đáp án D
y = x 3 − 3 m x 2 + 4 m 3 ⇒ y ' = 3 x 2 − 6 m x . Ta có y ' = 0 ⇔ x = 0 x = 2 m
Để hàm số đã cho có 2 điểm cực trị thì m ≠ 0. Khi đó
y ' = 0 ⇔ x = 0 ⇒ y 0 = 4 m 3 ⇒ A 0 ; 4 m 3 ∈ O y x = 2 m ⇒ y 2 m = 0 ⇒ B 2 m ; 0 ∈ O x
Vậy tam giác OAB vuông tại O nên S Δ O A B = 1 2 O A . O B ⇔ 4 = 1 2 4 m 3 2 m
⇔ m 4 = 1 ⇔ m = − 1 m = 1 ⇒ S − 1 ; 1

Đáp án C
Đạo hàm
y ' = 3 x 2 − 6 m x = 3 x x − 2 m ; y ' = 0 ⇔ x = 0 x = 2 m
Để đồ thị hàm số có hai điểm cực trị A, B <=> Phương trình y ' = 0 có hai nghiệm phân biệt x 1 , x 2 ⇔ 2 m ≠ 0 ⇔ m ≠ 0 .
Giả sử A 0 ; 3 m 2 và B 2 m ; 3 m 2 − 4 m 3 . Phương trình đường thẳng AB là:
x − 0 2 m − 0 = y − 3 m 2 3 m 2 − 4 m 3 − 3 m 2 ⇔ x = y − 3 m 2 − 2 m 2 ⇔ 2 m 2 x + y − 3 m 2 = 0
Lại có
A B = 2 m − 0 2 + 3 m 2 − 4 m 3 − 3 m 2 2 = 4 m 2 + 16 m 6 = 2 m 1 + 4 m 4
Suy ra
S Δ O A B = 1 2 A B . d O ; A B = 1 2 . 2 m . 1 + 4 m 4 . − 3 m 2 4 m 4 + 1 = 3 m . m 2
(đvdt).
Yêu cầu bài toán ⇔ S Δ O A B = 24 ⇔ 3 m 3 = 24 ⇔ m = 2 ⇔ m = ± 2 (thỏa mãn).

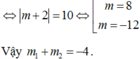
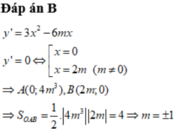
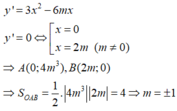


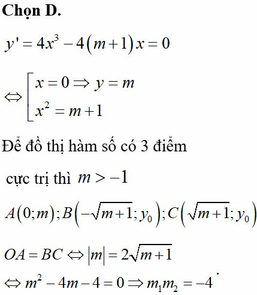

Đáp án B
Phương pháp:
Giải phương trình y’ = 0 tìm các điểm cực trị B, C của đồ thị hàm số và tính diện tích tam giác OBC.
Cách giải: TXĐ: D = R
Ta có: