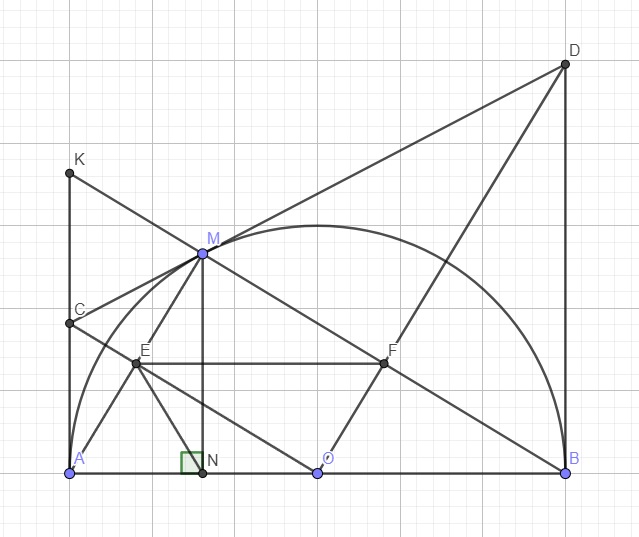
Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax của đường tròn (O). Trên cùng một nửa mặt
phẳng bờ AB có chứa tia Ax, lấy điểm M thuộc (0) (M khác A, M khác B sao cho MA > MB). Tiếp
tuyến của đường tròn (O) tại M cắt tia Ax tại E.
a) Chứng minh: 4 điểm A, E, M, O cùng thuộc một đường tròn
b) Gọi I là giao điểm của OE và AM. Chứng minh: OI.OE = R? và OE // MB
c) Gọi F là giao điểm của EB với đường tròn (O). Chứng minh: EFM = EMB

a: Xét tứ giác AEMO có
\(\widehat{EAO}+\widehat{EMO}=180^0\)
Do đó: AEMO là tứ giác nội tiếp