Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN//AC//BD

Bài 1:
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi

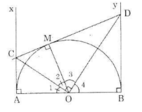
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)
b) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = AC, DM = BC
Do đó: CD = CM + DM = AC + BD (đpcm)
c) Ta có: AC = CM, BD = DM nên AC.BD = CM.MD
ΔCOD vuông tại O, ta có:
CM.MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC.BD = R2 (không đổi).

a: Xét(O) có
CM,CA là tiếp tuyến
nên CM=CA và OC là phân giác của góc AOM(1)
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
CD=CM+MD
=>CD=AC+BD
c: AC*BD=CM*MD=OM^2=R^2 ko đổi
d: CM=CA
OM=OA
=>OC là trung trực của AM
mà H nằm trên trung trực của AM
nên O,H,C thẳng hàng

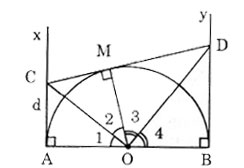 a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
nên CD=CA+DB
mình cần phần d, f