giúp tớ vớiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
4
cứu tớ vớiiii
18 tháng 3 2023
3:
độ dài cạnh là \(\sqrt{\dfrac{54}{6}}=\sqrt{9}=3\left(m\right)\)
V=3^3=27m3
17 tháng 1 2022
1: \(=\left(x+y+x-y\right)\left(x+y-x+y\right)=2x\cdot2y=4xy\)
2: \(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3=2y\left(3x^2+y^2\right)\)
3: \(=x^3+3x^2y+3xy^2+y^3+x^3-3x^2y+3xy^2-y^3\)
\(=2x^3+6xy^2=2x\left(x^2+3y^2\right)\)
4: \(=\left(7-4x+5\right)\left(7+4x-5\right)=\left(12-4x\right)\left(4x+2\right)\)
\(=8\left(3-x\right)\left(2x+1\right)\)
HT
1
14 tháng 5 2019
Ta có: \(\frac{1}{3^2}< \frac{1}{2.3}\)
\(\frac{1}{4^2}< \frac{1}{3.4}\)
.....................
\(\frac{1}{2014^2}< \frac{1}{2013.2014}\)
\(\Rightarrow A< \frac{1}{2^2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2013.2014}\)
Đặt \(B=\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2013.2014}\)
\(=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2013}-\frac{1}{2014}\)
\(=\frac{1}{2}-\frac{1}{2014}< \frac{1}{2}\)
\(\Rightarrow A< \frac{1}{2^2}+\frac{1}{2}=\frac{3}{4}\)
14 tháng 5 2019
\(\text{Ta có: }n^2>n^2-1=\left(n-1\right)\left(n+1\right)\)
\(\Rightarrow\frac{1}{n^2}< \frac{1}{\left(n-1\right)\left(n+1\right)}=\frac{1}{2}\left(\frac{1}{n-1}-\frac{1}{n+1}\right)\)
\(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+....+\frac{1}{2014^2}< \frac{1}{1.3}+\frac{1}{2.4}+\frac{1}{3.5}+...+\frac{1}{2013.2015}\)
\(=\frac{1}{2}\left(1-\frac{1}{3}\right)+\frac{1}{2}\left(\frac{1}{2}-\frac{1}{4}\right)+\frac{1}{2}\left(\frac{1}{3}-\frac{1}{5}\right)+...+\frac{1}{2}\left(\frac{1}{2013}-\frac{1}{2015}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{2013}-\frac{1}{2015}\right)\)
\(=\frac{1}{2}\left(1+\frac{1}{2}-\frac{1}{2014}-\frac{1}{2015}\right)\)
\(=\frac{1}{2}\left(\frac{3}{2}-\frac{1}{2014}-\frac{1}{2015}\right)\)
\(=\frac{3}{4}-\frac{1}{2}\left(\frac{1}{2014}+\frac{1}{2015}\right)< \frac{3}{4}\)
Vậy .............
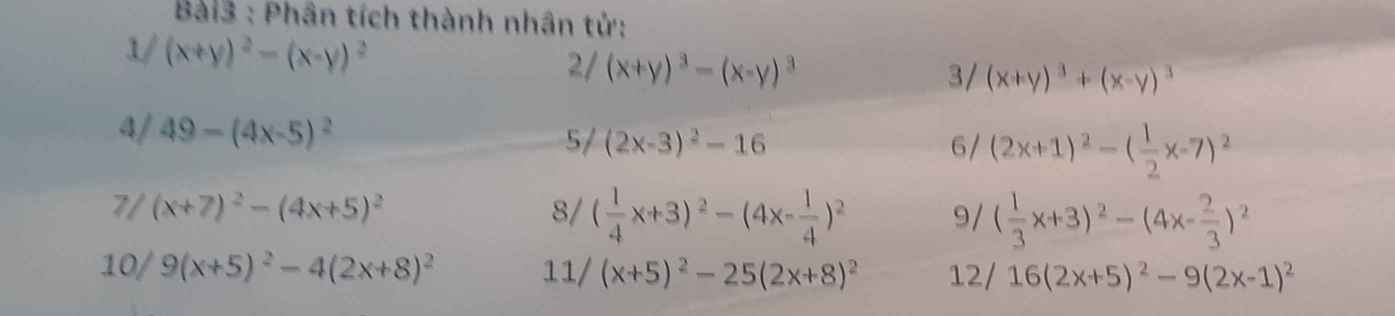
Thi tự làm đi ạ
a: \(=10\sqrt{3}-12\sqrt{3}+3\sqrt{3}=\sqrt{3}\)