câu này làm sao vậy ạ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 4 2022
vì sao nó lên câu trả lời để mình hỏi mà sao nó cứ lên mua tài khoản vid
N
0
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2021
\(\overrightarrow{MN}=\left(2;2\right)\Rightarrow MN=\sqrt{2^2+2^2}=2\sqrt{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\sqrt{2}\)
Gọi I là tâm đường tròn đường kính MN \(\Rightarrow\) I là trung điểm MN
\(\Rightarrow I\left(0;2\right)\)
Phương trình (C): \(x^2+\left(y-2\right)^2=2\)
b.
Tiếp tuyến d' song song d nên nhận \(\left(3;-5\right)\) là 1 vtpt
Phương trình d' có dạng: \(3x-5y+c=0\)
d' là tiếp tuyến của (C) nên: \(d\left(I;d'\right)=R\)
\(\Leftrightarrow\dfrac{\left|3.0-5.2+c\right|}{\sqrt{3^2+\left(-5\right)^2}}=\sqrt{2}\Leftrightarrow\left|c-10\right|=2\sqrt{17}\)
\(\Rightarrow\left[{}\begin{matrix}c=10+2\sqrt{17}\\c=10-2\sqrt{17}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}3x-5y+10+2\sqrt{17}=0\\3x-5y+10-2\sqrt{17}=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 6 2021
Gọi I là trung điểm AB \(\Rightarrow\dfrac{IM}{SI}=\dfrac{1}{3}\) theo t/c trọng tâm
Trong tam giác SAB, từ M kẻ đường thẳng song song SA cắt AB tại H
\(\Rightarrow MH\perp\left(ABC\right)\Rightarrow NH\) là hình chiếu vuông góc của MN lên (ABC)
\(\Rightarrow\widehat{MNH}\) là góc giữa MN và (ABC)
Talet: \(\dfrac{MH}{SA}=\dfrac{IH}{IA}=\dfrac{IM}{SI}=\dfrac{1}{3}\Rightarrow\left\{{}\begin{matrix}MH=\dfrac{2a}{3}\\IH=\dfrac{2a}{9}\end{matrix}\right.\)
\(IC=\sqrt{IB^2+BC^2}=\dfrac{a\sqrt{21}}{2}\) \(\Rightarrow IN=\dfrac{1}{3}IC=\dfrac{a\sqrt{21}}{6}\)
\(cos\widehat{BIC}=\dfrac{IB}{IC}=\dfrac{\sqrt{21}}{7}\Rightarrow cos\widehat{AIC}=-\dfrac{\sqrt{21}}{7}\)
\(NH=\sqrt{IN^2+IH^2-2IN.IH.cos\widehat{AIC}}=\dfrac{a\sqrt{277}}{18}\)
\(\Rightarrow tan\widehat{MNH}=\dfrac{MH}{NH}\approx0,721\Rightarrow\widehat{MNH}\approx36^0\)
Không đáp án nào đúng?
MH
10 tháng 1 2022
\(\sqrt{\left(1-\sqrt{2}\right)^2}\sqrt{\left(1+\sqrt{2}\right)^2}\)
\(=\sqrt{\left(1-\sqrt{2}\right)^2\left(1+\sqrt{2}\right)^2}\)
\(=\sqrt{\left(1-2\right)^2}=\sqrt{\left(-1\right)^2}=1\)
10 tháng 1 2022
Câu 21: D
Câu 15: \(=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\)
Câu 11: \(=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{6}=\dfrac{3+\sqrt{3}}{6}\)
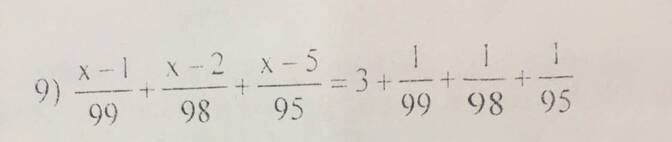
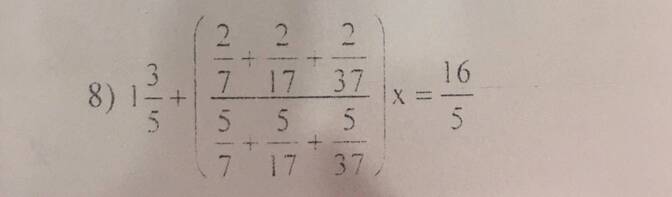
`2/(x+1)+x/(3x+3)=1`
`ĐK:x ne -1`
`pt<=>6/(3x+3)+x/(3x+3)=1`
`<=>(x+6)/(3x+3)=1`
`<=>x+6=3x+3`
`<=>2x=2`
`<=>x=1(TM)`
Vậy pt có 1 nghiệm
Câu này em quy đồng rồi giải phương trình em nhé!