Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mình sẽ không vẽ hình vì sợ duyệt.
Vì (O) có bán kính 10cm nên \(OA=10cm\)
Gọi OH là khoảng cách từ O đến AB, khi đó theo quan hệ vuông góc giữa đường kính và dây, ta có H là trung điểm AB, từ đó \(AB=2AH\)
Đồng thời, \(OH=8cm\)
\(\Delta OAH\)vuông tại H \(\Rightarrow AH=\sqrt{OA^2-OH^2}=\sqrt{10^2-8^2}=6\left(cm\right)\)
\(\Rightarrow AB=2AH=2.6=12\left(cm\right)\)
\(\Rightarrow\)Chọn A
Đáp án: B. 8cm
Lời giải:
Gọi dây trên là dây AB. Hạ OH\(\perp\)AB = {H} (cd)
Xét (O) 1 phần đường kính OH: OH\(\perp\)AB = {H} (cd)
=> H là trung điểm AB (đl) => HA = HB = AB: 2 = 12:2 = 6 (cm)
OH\(\perp\)AB = {H} (cd) => \(\Delta\)OHB vuông tại H (đn)
=> OH\(^2\)+ HB\(^2\)= OB\(^2\)(Đl Py-ta-go)
T/s: OH\(^2\)+ 6\(^{^2}\)= R\(^2\)
<=> OH\(^2\)+36 = 10\(^2\)=100
<=> OH\(^2\)= 64 => OH = 8 (cm)
\(^2\)
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)
Đáp án C
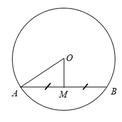
Vì M là trung điểm của AB nên ta có: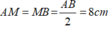 
Theo quan hệ vuông góc giữa đường kính và dây ta có;
Mà khoảng cách từ O đến AM bằng 6 cm nên OM = 6 cm
Áp dụng định lí pytago vào tam giác OAM vuông ta có:
O A 2 = O M 2 + A M 2 = 6 2 + 8 2 = 100 n ê n O A = 10 c m
Suy ra: bán kính đường tròn đã cho là R = 10 cm.
Vì \(AB\perp MN\) tại H nên H là trung điểm AB (dây vuông góc đường kính)
\(\Rightarrow AH=\dfrac{1}{2}AB=6\left(cm\right)\)
MH vừa là đường cao vừa là trung tuyến nên \(\Delta MAB\) cân tại M
Do đó \(MA=MB=10\left(cm\right)\)
Ta có \(\widehat{MAN}=90^0\)(góc nt chắn nửa đường tròn) nên tam giác MAN vuông tại A
Áp dụng HTL tam giác
\(\dfrac{1}{AH^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\\ \Rightarrow\dfrac{1}{36}=\dfrac{1}{AN^2}+\dfrac{1}{100}\\ \Rightarrow\dfrac{1}{AN^2}=\dfrac{1}{36}-\dfrac{1}{100}=\dfrac{4}{225}\\ \Rightarrow4AN^2=225\Rightarrow AN^2=\dfrac{225}{4}\Rightarrow AN=\dfrac{15}{2} =7,5\left(cm\right)\)
\(MN=\sqrt{AN^2+AM^2}=\sqrt{10^2+7,5^2}=12,5\left(cm\right)\)
Vậy đường kính đường tròn \(\left(O\right)\) dài 12,5 cm
NH vừa là đường cao vừa là trung tuyến nên \(\Delta NAB\) cân tại N
OK vuông góc với MB nên K cũng là trung điểm MB
\(\Rightarrow AN=NB=7,5\left(cm\right)\)
\(\left\{{}\begin{matrix}NO=OM\left(=R\right)\\MK=KB\left(cm.trên\right)\end{matrix}\right.\Rightarrow OK\) là đtb tam giác MBN
\(\Rightarrow OK=\dfrac{1}{2}NB=\dfrac{1}{2}\cdot7,5=3,75\left(cm\right)\)
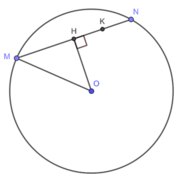
Ta có tam giác MON cân tại O
Mà ∠ OMN = 45 ° suy ra, tam giác OMN vuông cân tại O
OH là đường cao của tam giác MON
Suy ra, OH là đường trung tuyến của tam giác MON
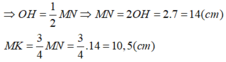
Đáp án: A
D
Chọn D