Cho tam giác ABC có phân giác AM. Từ M kẻ MQ vuông góc với AB, kẻ MP vuông góc với AC ( Q thuốc AB, P thuộc AC), AM cắt QP ở H. CMR:
a) Tứ giác AQMP nội tiếp
b) Tam giác MQP cân
c) Tam giác HAP đồng dạng với HQM
CM giúp em câu b và c là đc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 2 2023
#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM` chung
`AB = AC (g``t)`
\(\widehat{AMB}=\widehat{AMC}=90^0\)
`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`
`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`
`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`
`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`
`=> AM` là tia phân giác của \(\widehat{BAC}\)
`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:
`AM` chung
\(\widehat{HAM}=\widehat{KAM}(CMT)\)
`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`
`=> AH = AK (2` cạnh tương ứng `)`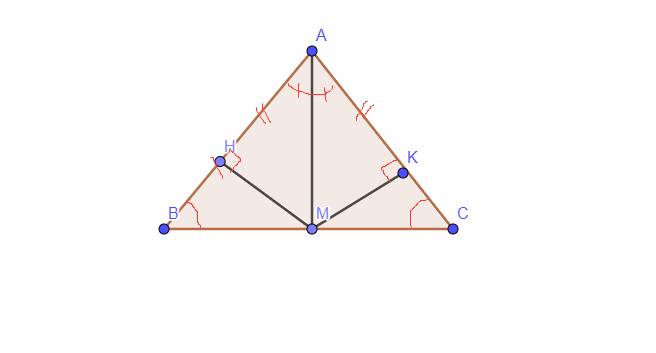
DT
20 tháng 3 2019
a, xét tam giác AMB và tam giác AMC có:
AB=AC(gt)
\(\widehat{BAM}\) =\(\widehat{CAM}\)(gt)
AM chung
suy ra tam giác AMB= tam giác AMC(c.g.c)
b,xét tam giác AHM và tam giác AKM có:
AM cạnh chung
\(\widehat{HAM}\)=\(\widehat{KAM}\)(gt)
suy ra tam giác AHM=tam giác AKM(CH-GN)
Suy ra AH=AK
c,gọi I là giao điểm của AM và HK
xét tam giác AIH và tam giác AIK có:
AH=AK(theo câu b)
\(\widehat{IAH}\)=\(\widehat{IAK}\)(gt)
AI chung
suy ra tam giác AIH=tam giác AIK (c.g.c)
Suy ra \(\widehat{AIH}\)=\(\widehat{AIK}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AIH}\)=\(\widehat{AIK}\)= 90 độ
\(\Rightarrow\)HK vuông góc vs AM
21 tháng 1 2022
a: Xét ΔABM vuông tại M và ΔACN vuông tại N có
AB=AC
\(\widehat{BAM}\) chung
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
b: Xét ΔAMN có AM=AN
nên ΔAMN cân tại A
21 tháng 1 2022
a) Xét tam giác BNC vuông tại N và tam giác CMB vuông tại M:
BC chung.
\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A).
=> Tam giác BNC = Tam giác CMB (cạnh huyền - góc nhọn).
=> BN = CM (2 cạnh tương ứng).
Ta có: AB = AN + BN; AC = AM + CM.
Mà AB = AC (Tam giác ABC cân tại A); BN = CM (cmt).
=> AM = AN.
b) Xét tam giác AMN: AM = AN (cmt).
=> Tam giác AMN cân tại A.
c) Xét tam giác ABC:
BM; CN là đường cao (BM vuông góc với AC; CN vuông góc với AB).
I là giao điểm của BM và CN (gt).
=> I là trực tâm.
=> AI là đường cao.
Mà AI là đường cao xuất phát từ đỉnh A của tam giác ABC cân tại A.
=> AI là đường phân giác góc A (Tính chất các đường trong tam giác cân).
2 tháng 4 2021
b) Sửa đề: C/M ΔMPQ cân
Xét ΔAPM vuông tại P và ΔAQM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)(AM là tia phân giác của \(\widehat{PAQ}\))
Do đó: ΔAPM=ΔAQM(cạnh huyền-góc nhọn)
Suy ra: PM=QM(hai cạnh tương ứng)
Xét ΔMPQ có MP=MQ(cmt)
nên ΔMPQ cân tại M(Định nghĩa tam giác cân)
10 tháng 1 2022
Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật
mà AM là tia phân giác
nên AHMK là hình vuông
a) Xét tứ giác AQMP có
\(\widehat{AQM}\) và \(\widehat{APM}\) là hai góc đối
\(\widehat{AQM}+\widehat{APM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AQMP là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔAQM vuông tại Q và ΔAPM vuông tại P có
AM chung
\(\widehat{QAM}=\widehat{PAM}\)(AM là tia phân giác của \(\widehat{QAP}\))
Do đó: ΔAQM=ΔAPM(cạnh huyền-góc nhọn)
Suy ra: QM=PM(hai cạnh tương ứng)
Xét ΔMQP có QM=PM(cmt)
nên ΔMQP cân tại M(Định nghĩa tam giác cân)
giúp em câu c với